ブログラミング のブログ記事一覧 裏 Rjpwiki
この公式はアレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられるが、現代ではこれ自体は シラクサ の アルキメデス にも既知であったと三平方の定理の内容:直角三角形と辺の長さの関係 まず、三平方の定理とは何なのでしょうか。 古代ギリシャの数学者、ピタゴラスが証明した公式が三平方の定理(ピタゴラスの定理)です。 三
ピタゴラスの定理 公式
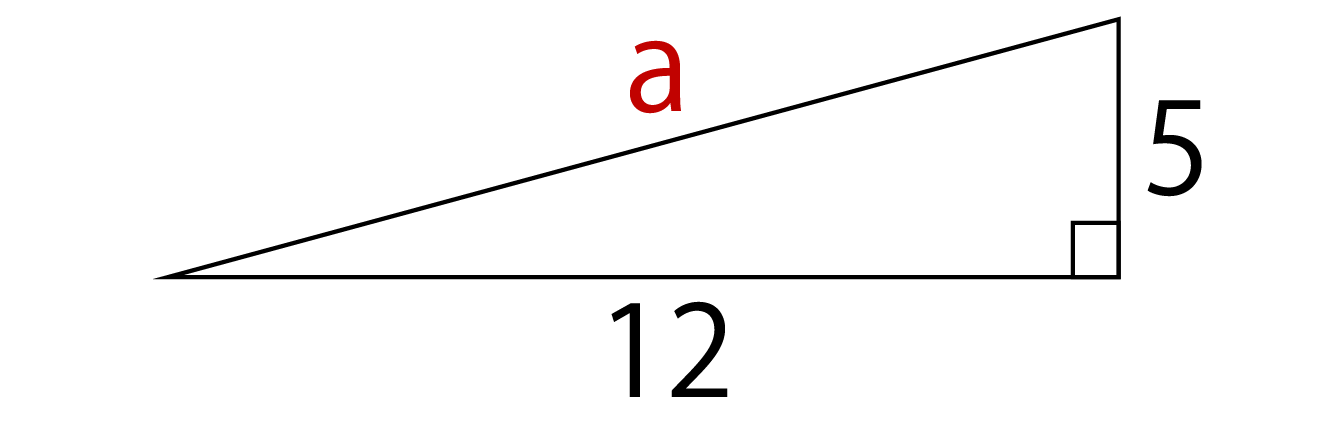
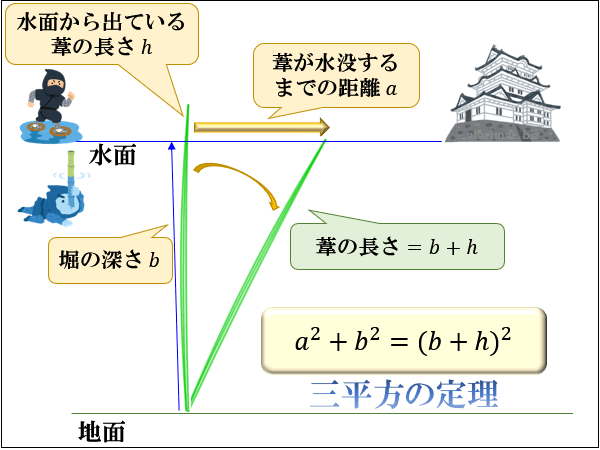
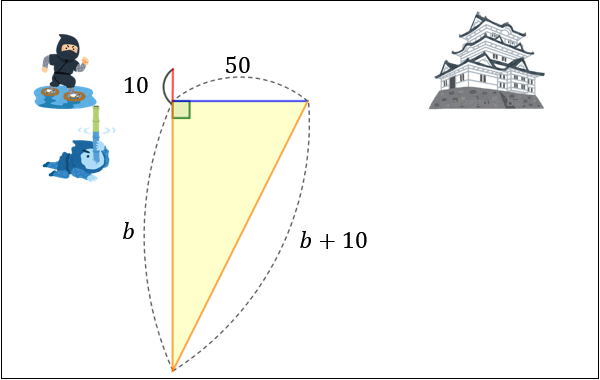
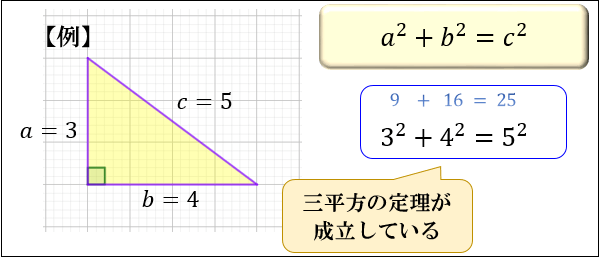
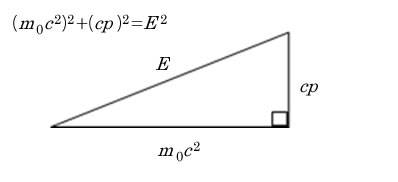
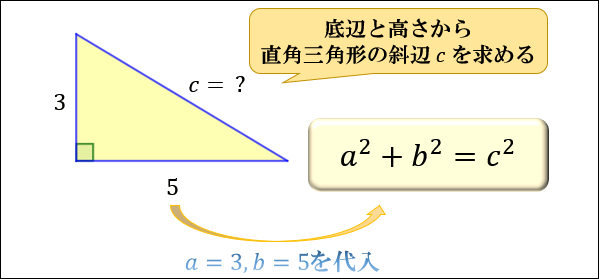
ピタゴラスの定理 公式-ピタゴラスの定理とは? ピタゴラスの定理とは、直角三角形の底辺の2乗と高さの2乗の合計が、斜辺の2乗に等しいという定理です。下記にピタゴラスの定理を示しました。 x 2 y 2 =z 2 xを底辺コラム ピタゴラスの定理 直角三角形の3辺の長さに関する a 2 b 2 =c 2 という関係は ピタゴラスの定理 (三平方の定理)と呼ばれます。 この定理はその名の通り古くから知られていますが、本当

Dockerのslaveコンテナ起動エラー Javaが見つからない ロレンスブログ
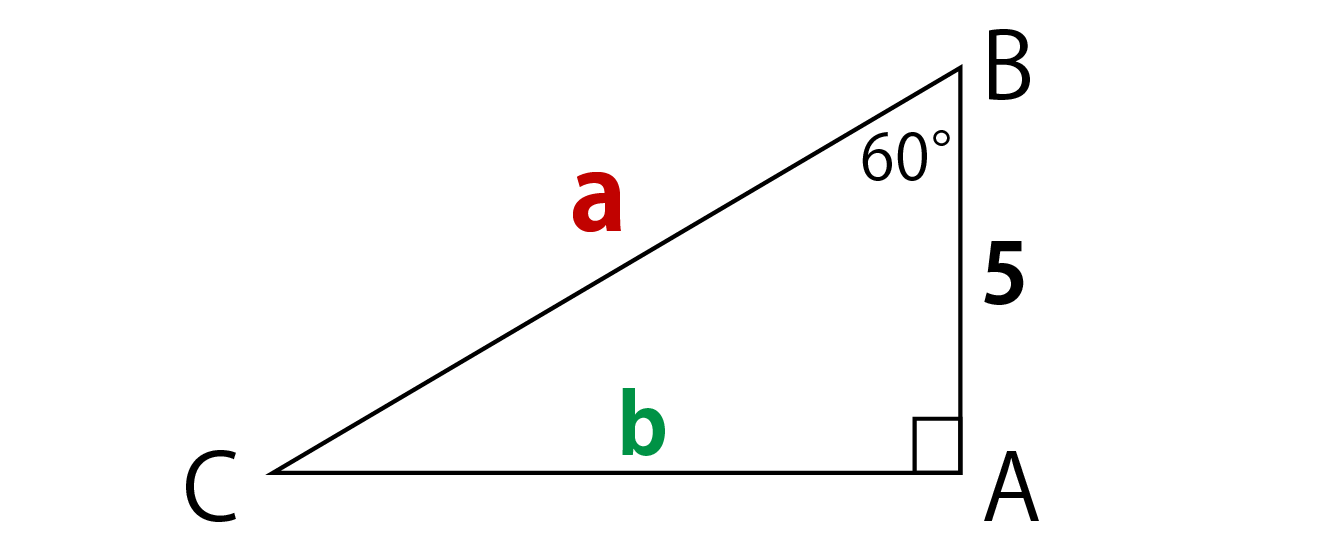
ピタゴラスの基本三角関数公式 (1) \ \cos^{2}x\sin^{2}x=1 \ (2) \ 1\tan^{2}x=\cos^{2}x \ (3) \ 1\cot^{2}x=\sin^{2}x \ユークリッドによる「ピタゴラスの定理(三平方の定理)」の証明です。Euclid's proof of The Pythagorean Theoremその他の動画#1レオナルド・ダ・ヴィン 直角三角形において、「直角」をはさむ2つの辺の長さを a, b 、斜辺の長さを c としたとき a 2 b 2 = c 2 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピ
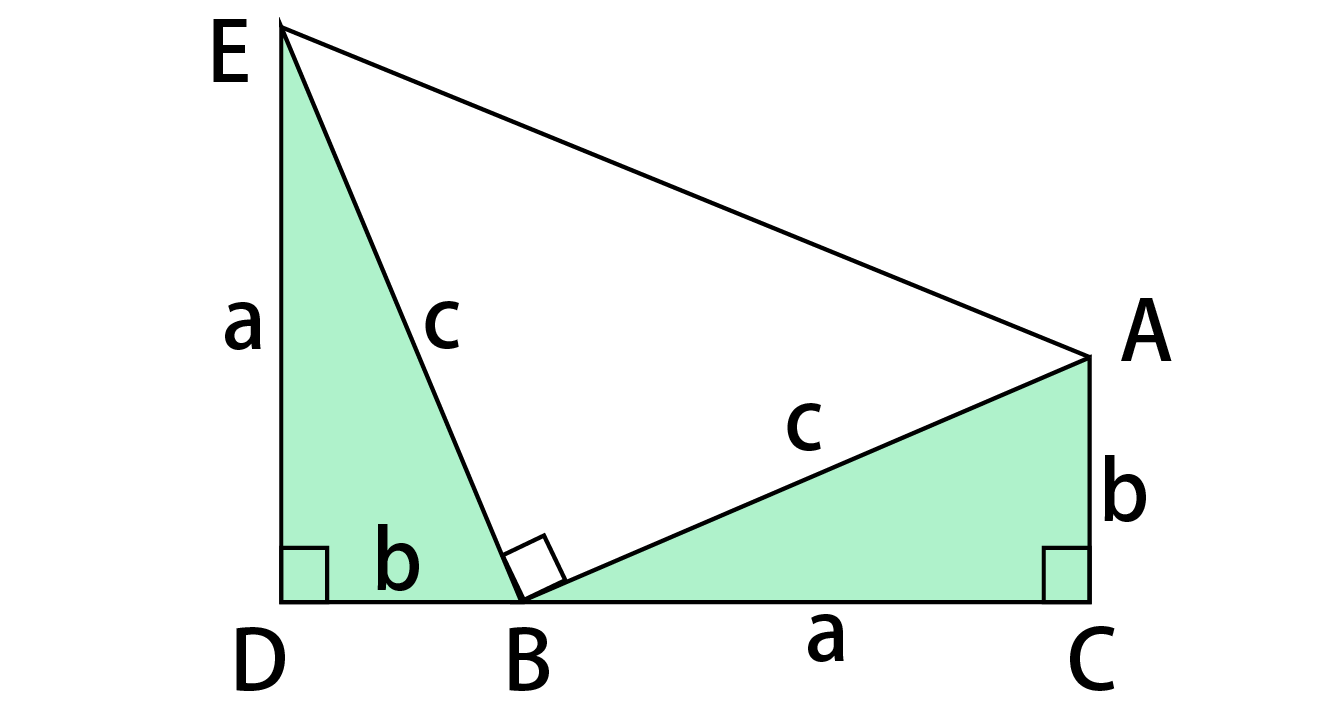
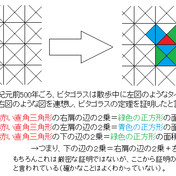
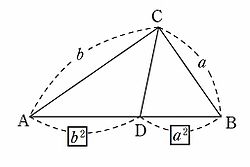
原始ピタゴラス数の公式$$a=m^2n^2 , b=2mn , c=m^2n^2$$これは絶対に覚える! 前提条件で重要なのは、「 $mn$ が奇数であること」「 $m$ と $n$ が互いに素な自然数であること」の $2$ ピタゴラスの定理の証明 この定理には数百通りもの異なる 証明 があり、例えば、「以下では頂点 A, B, C からなる三角形を ABC と表す」「各辺 AB, BC, CA に向かい合う角をそれぞ三平方の定理(ピタゴラスの定理): \angle C=90^ {\circ} ∠C = 90∘ であるような直角三角形において, a^2b^2=c^2 a2 b2 = c2 英語ですが,三平方の定理の証明を105個解説しているすさまじ
ピタゴラスの定理 公式のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 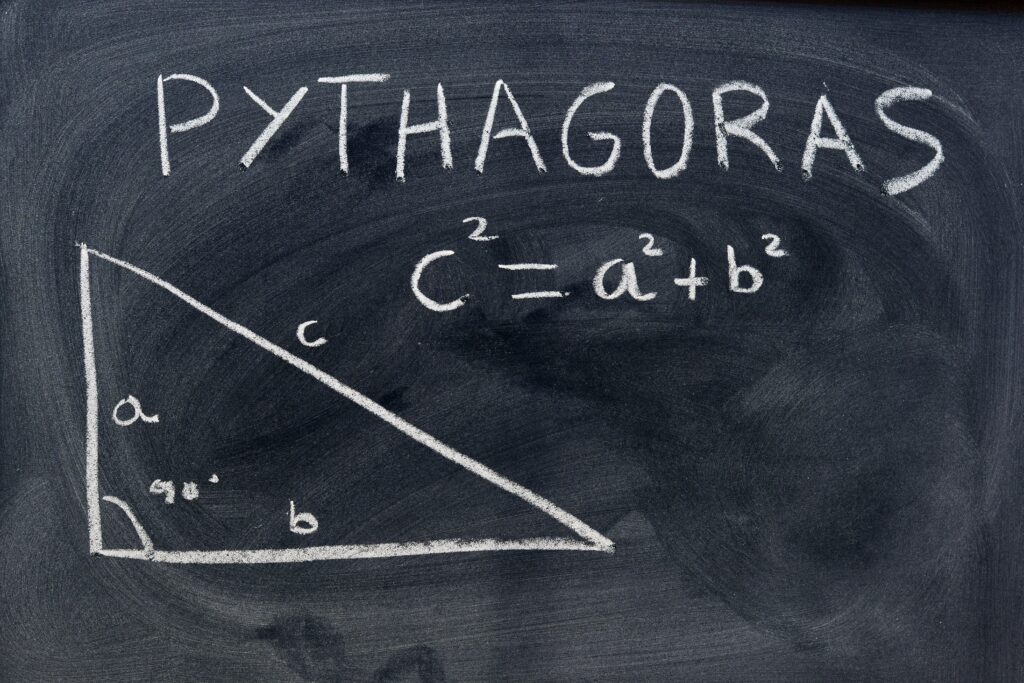 |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | 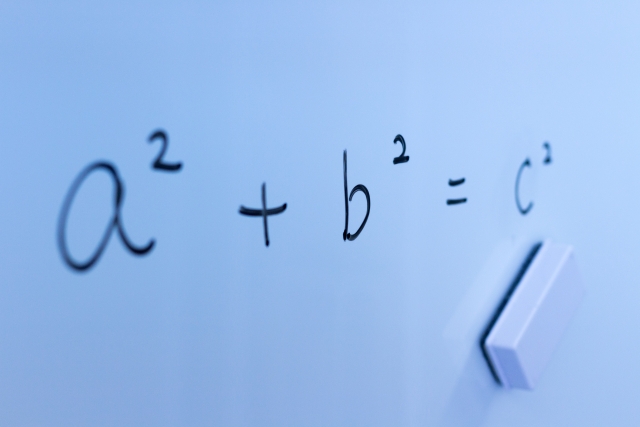 |  |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 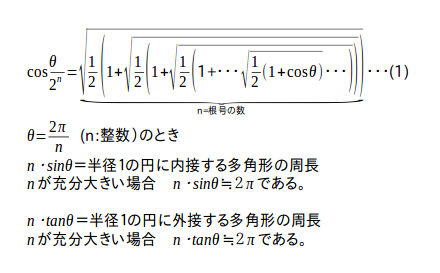 |  |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 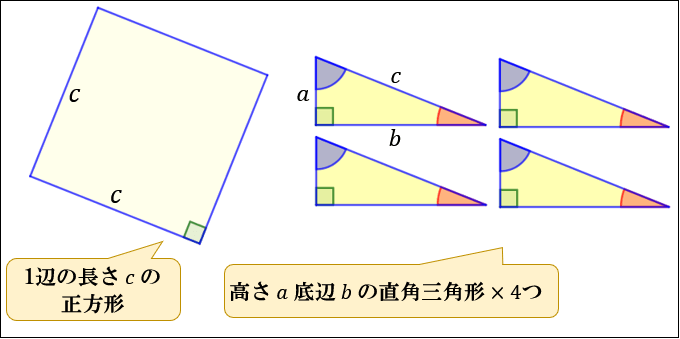 | 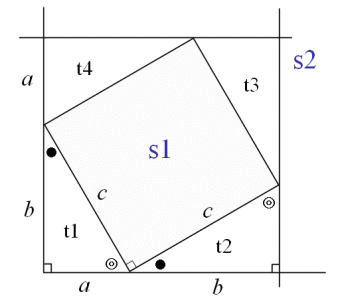 |
 |  | 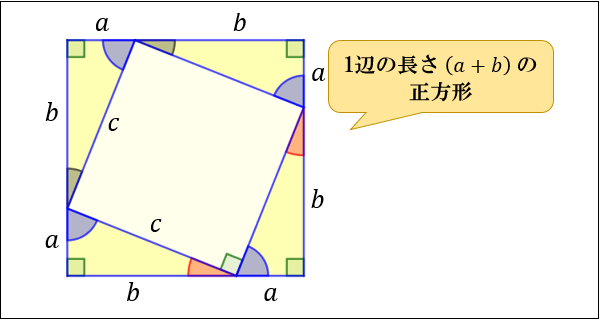 |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 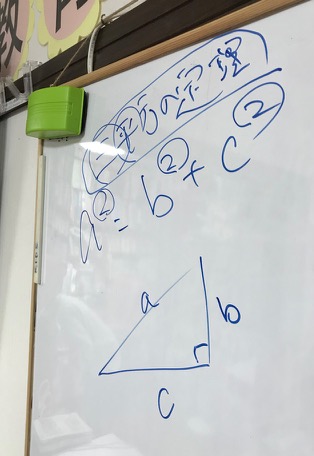 |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「ピタゴラスの定理 公式」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
三角比と三角関数の公式の整理と歴史的背景単元まとめ 数学Iの授業で三角比を伝えると思います(伝えられると思います)。 いきなり、サインコサイン 歴史 三平方の定理は別名「ピタゴラスの定理」と呼ばれています。 しかし、実際にこの定理を発見したのはピタゴラス(Pythagoras, BC569頃BC500頃)ではなく、彼が生まれる
Incoming Term: ピタゴラスの定理 公式,




0 件のコメント:
コメントを投稿