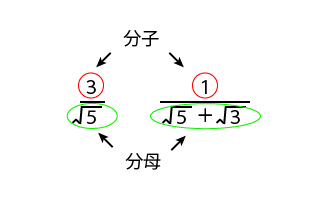
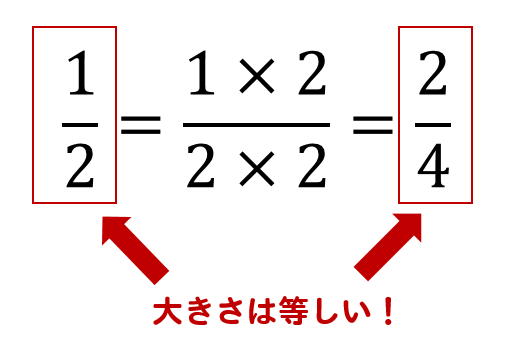
入試数学コンテスト 実は,この分数不等式は 方法1.分母を払う方法 以外にも 方法2.通分する方法(おすすめ) や 方法3.両辺のグラフを描く方法 といった解き方があります分数というのは、分母と分子の両方に同じ数を掛けるのであれば 大きさは変わらないという特徴があったよね! だから、分母と分子の両方に同じルートを掛けることで 分数の大きさを変えることなく 見た目だけをチェンジすることができるってわけ!右辺は分数の形式ですので、数式ツール リボンのデザインタブで分数→分数(縦)を実行します。 分数(縦)が入力されました。 分母に入力したいのでカーソルキーを使って分母の四角を選択します。 「2a」と入力します。カーソルキーで分子の四角を選択

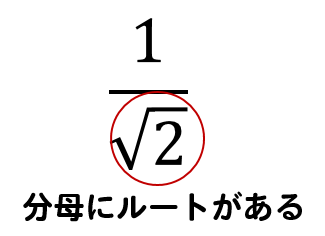
答えが分数のとき 分母にルートがあったら消す のように分母がマイナスのときはプラスに Clear
分母が分数 ルート
分母が分数 ルート- 分数の足し算 分数の足し算は ①:2つの分数の「分母」が同じになるようにそろえて(通分して)から ②:2つの分数の「分子」を足し算をして ③:最後に「約分」をする。 この 3つのステップをふむのがコツ です。 ここでは、「2/3 1/12」を計算してみましょう。はよい子なので,そのままで使えます.片方(本当は半分ではなくルートだが言いにくいので通俗的に)しかなくて悪い子は だけです. だから,下に書いた答案のように,片方しかない だけをもう一枚付けて の1枚にするのです. お薦めの答案 (答) (3) のように分母の根号が簡単になる場合は,初めに根号を簡単にしてから,次に分母の処理をします




ルートの整数部分と小数部分 すうがくのいえ
※19年4月6日(土) →誤字を修正しました。 分数を使いこなそうシリーズ第2弾! 算数・数学が苦手な皆さん、分数のいろいろな計算のやり方を覚えて慣れて、計算得意になっちゃいましょう! 今回は、分数のかけ算・わり算に注目していきたいと思います。 「② 分母にあるルートを、分母・分子に掛ける」 からいきます。 分母に \( \sqrt{3} \) があるので、 分母・分子に \( \sqrt{3} \) を掛けます 。 \( \begin{align} \displaystyle \frac{2}{\sqrt{3}} & = \frac{2}{\sqrt{3}} \color{blue}{ \times \frac{\sqrt{3}}{\sqrt{3}} 普通は「分母を有理化(ルートをなくす)」して、分母にはルートがない形にします。 2/√ (5/3) = 2√3 /√5
「ルートの内側の数字同士は割る事が出来る」ことを思い出しましたか? つまり、 分数の割り算も、分母・分子は割ることが出来ましたね、それと一緒です。 この計算が出来れば、ルートの割り算は80%理解できたも同然です、ご安心ください。 ってことは、こいつらを√2でわれるから、 5分の√ × √ (2分の15) = 5分の √10 × √ ( 1分 の15) になる。 Step3 分母・分子どうしを掛け算 分母・分子どうしで掛け算しよう。 ルートの掛け算の仕方 をつかってみてね。 例題でも、分母・分子それぞれ計算すると、見た目は少し複雑ですが、難しいことはしていません。 f(x) g(x) の導関数は、 lim h → 01 h{f(x h) g(x h) − f(x) g(x)} です。 ここで、 {} の中身は以下のように変形できます: f(x h)g(x) − f(x)g(x h) g(x h)g(x) (通分した) = f(x h)g(x) − f(x)g(x) g(x h)g(x) f(x)g(x) − f(x)g(x h) g(x h)g(x) (同じもの f(x)g(x) を引いて足した)
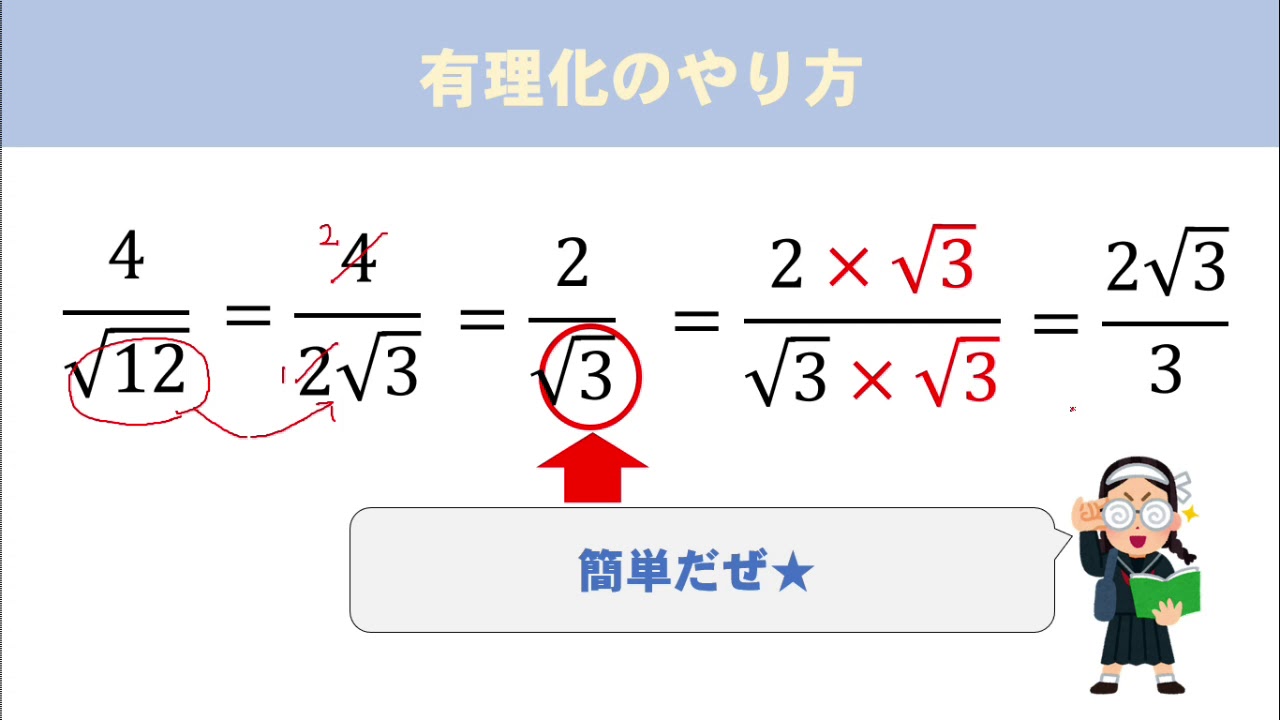
分母に分数を含む式 ここでは、分母に分数を含む式の計算のしかたについてみていきましょう。 難しい分数式を考える前に、簡単な分数を例に考えてみましょう。 この分数式について考えてみます。 そもそも分数A/Bとは、"A÷B"を簡単にまとめたものでしたね。 このことから であることがわかります。 あとはこの式を計算すると 設問の問題も、これと同じ考え算数数学個別指導の中山先習塾の映像授業です。 高1「実数、無理数、根号、ルート、計算規則、分母の有理化」 中山先習塾の公式サイト( https分母の有理化1 分数の分母に平方根がある場合に分母の平方根をなくすことを 有理化 という。 解説動画 ≫ 分母を有理化せよ。 5 3 7 8 9 5 12 ① 5× 3 3 × 3 = 5 3 3 a × a =aという性質を利用して、 分母にある√と同じ√を 分母、分子にかける。




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ




平方根 ルート の計算をおぼえよう しろカスと学ぶ中学数学 理科
数学 分母にルートの分数がある場合の計算を教えてください! 下の計算はどうやってやるのか教えてくださ 数学 例えば16の4分の3乗は? 数学 4 数学の質問です。分数関数の分母に二乗がついていた場合はどのように計算したら良いのでしょうか? 二次分 数学 5 分数 とルートの計算 分数関数は不等式や微分積分に登場したり、グラフの問題で登場したりします。 グラフの問題では、 一次分数関数が出てくることが多い です。 一次分数関数の基本形 分母と分子が \(x\) の一次式である関数を、「一次分数関数」といいます。 分母の平方根が2乗されてルートがとれるんだ。 たとえば、「√a分のb」って分数がいたとしよう。 分母・分子に√aをかければいいのさ。 すると、 √a分のb = (√a×√a)分の(b×√a) = a分の(b√a) になるね! 例題の分数の分母は、



有理化 もう一度やり直しの算数 数学



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋
ルートの付く数があるといっても分数やルートの計算ルールは変わりません。分数の計 1000 第10回(放送日:9月28日、10月5日) 分数詐欺のトリックを見やぶれ ~分母が異なる足し算~ タルトを分数の大きさで提供するお店に通う 分数についての理解を深めるとともに、同分母の分数の加法分子も分母も関数の分数関数 さて、それではこのような分数関数の微分はどのようにして求めるのでしょうか?次から見ていきましょう。 2 分数の微分のやり方 結論から言うと、分数の微分はどちらも公式を使って求めることができます。それぞれ見て分母分子に 3 をかけることによって、分母のルートが外せます: 1 3 = 1 × 3 3 × 3 = 3 3 このように、分母が n という形の分数については、 分母分子にそれぞれ n をかける ことによって分母を有理化することができます。




2の平方根 Wikipedia




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
計算しましょう。 √2 2 √5√2 2 2 5 2 後ろの分数の分母を有理化して計算すればなんてことはないですね。 まずは有理化してから計算してみましょう。 √2 2 √5√2 2 2 5 2 = √2 2(√5−√2) (√5√2)(√5−√2) = 2 2 ( 5 − 2) ( 5 2) ( 5 − 2) = √2 2(√5−√2) 3 = 2 2 ( 5 − 2) 3 = 3√2 3 2(√5−√2) 3 = 3 2 3 2 ( 5 − 2) 3 = 3√22√5−2√2 3 = 3 2 2 5 − 2 2 3分母がマイナスの時の分数の扱い 数学の基本 分母がマイナスの時の分数の扱い 数学の基本 Watch later Share Copy link Info Shopping Tap to unmute 冒頭のように、分母にルートがある分数を変形して、分母にルートがないようにすることを「有理化」と言います。 例えば、$\dfrac{2}{\sqrt{3}}$ を考えてみましょう。「2乗するとルートが消える」ので、分母分子に $\sqrt{3}$ を掛ければいいですね。よって



根号計算 約分




ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく
1±33± 6, 3, 6はいずれも3で割り切れるので(最大公約数は3だから),分母・分子を3で割ります. ※「約分する前に( )でくくる」方式で行うときは 問3HELP −3±−1±3 3, 6, 6はいずれも3で割り切れるので(最大公約数は3だから),分母・分子を3で割ります. ※「約分する前に( )でくくる」方式で行うときは 問4HELP 2±2±63±44±312±ツイート 無料ダウンロード・印刷できる小学5年生の算数プリント。 分母のちがう分数を、通分、約分して引き算する練習問題です。 異分母の分数の引き算(1) 答え 異分母の分数の引き算(2) 答え 異分母の分数の引き算(3) 答え ルート10の連分数表記 本稿では、 √10 10 の連分数表記について見ていきます。 まず、次の式をご覧ください。 中学のとき、分母に 無理数 が来たときは有利化しなさいと習いましたが、ここではその逆を行っています。 3 √10 = 6 1 3√10 (2) (2) 3 10 = 6 1 3 10 となります。 ここで、式 (2)の右辺に現れた 3√10 3 10 に、式 (2)を代入します。 式 (3)の右辺




分母の有理化の方法 数学の偏差値を上げて合格を目指す




部分分数分解のやり方と公式 5パターンの問題から分かる変形のコツ アタリマエ
5分のルート2=ルート25分のX ルート5分の2=ルート25分のX という問題で、答えは2となのですが、どうしてそうなるのかが分かりません 。やり方も分かりません。 あと、ルートが分母と分子両方についた分数で、分母の数が同じとき、どうやって数の大小を判断しますか? 分かりにくルートの付く数があるといっても分数やルートの計算ルールは変わりません。分数の計算は下記が参考になります。 分数とは?1分でわかる意味、分母、分子、約分、掛け算と割り算の解き方 ただし分母にルートの付く数がある場合、有理化(ゆうりか)を行い、より簡単な形で表します分母の有理化のやり方はこれでバッチリ! ルートの計算方法まとめ!問題を使って徹底解説! ルートの分数計算、問題解説で完全マスターだ!←今回の記事 整数部分、小数部分の求め方!分数の場合に




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ
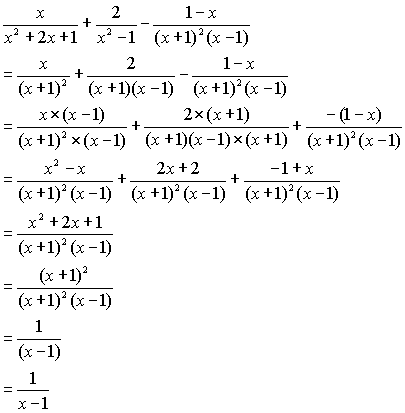



分数の復習と分数式の計算
分数の分母が分数であり、その分母がルートの場合の計算の仕方がよくわかりません。言葉では紛らわしい言い方になってしまいますが、画像の3がルートの場合というような感じです。 もし3が√3 だとしたら、 分母と分子に√3をかけたとき分母は√3×√有理化とは、分数の分母のルートをなくす方法のことです。 この式の場合の有理化をする方法は√7を分子と分母に掛け合わせることです。 有理化してみると、√35/7になりました。 √35はこれ以上簡単にできないので、答えは、√35/7です。平方根 (ルート)の計算方法まとめ。 おさえておくべき4つのポイント Tooda Yuuto 17年9月日 / 18年11月10日 このページでは、平方根の足し算・引き算・かけ算・割り算を4つのポイントに分けて解説していきます。 スポンサーリンク 目次 ①ルートの中身




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




実数 ルート を有理化する意味はこれでわかる 分母に がngの巻 Vol 9 3回読めば 絶対理解できる看護受験数学 Kazアカデミー 大阪の看護学校 看護予備校
分数コードのルート of ピアノ弾き語り教室 コードの仕組みを知ろう! 分数コード 分数コードでは、分母が左手(ベース音)、分子がコードになります。 ですので、左手は分母を弾けば良いという事少数や分数を含んだ数式の展開にも対応しています。 約分の電卓 分母と分子を入力すると約分された分数を表示する電卓です。大きい数の分数でも簡単に約分をおこなうことができます。 通分の電卓 分数を通分できる電卓です。3つ以上の分数を通分する




4 のlog36の 乗てどうしてルート6になるんですか Clear



平方根 分母の有理化のやり方はこれでバッチリ 数スタ



ルート の分数計算教えてください すみません 急ぎです Yahoo 知恵袋




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ
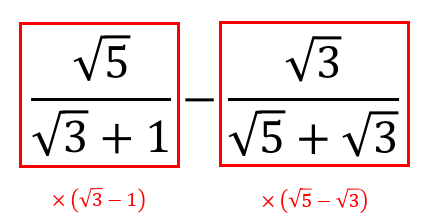



ルートの分数計算 問題解説で完全マスターだ 数スタ



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo




高校数学 数列の極限 無理式の極限 受験の月




分数分の分数 分母と分子 上と下 に分数があるときのやり方を解説 数スタ




三項の有理化 高校数学 Youtube




ルートの整数部分と小数部分 すうがくのいえ




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




高校数学 繁分数式 分数の分数 の計算 受験の月




ルートの中を簡単にする と 分母の有理化 を比べる とちぎeライブラリ
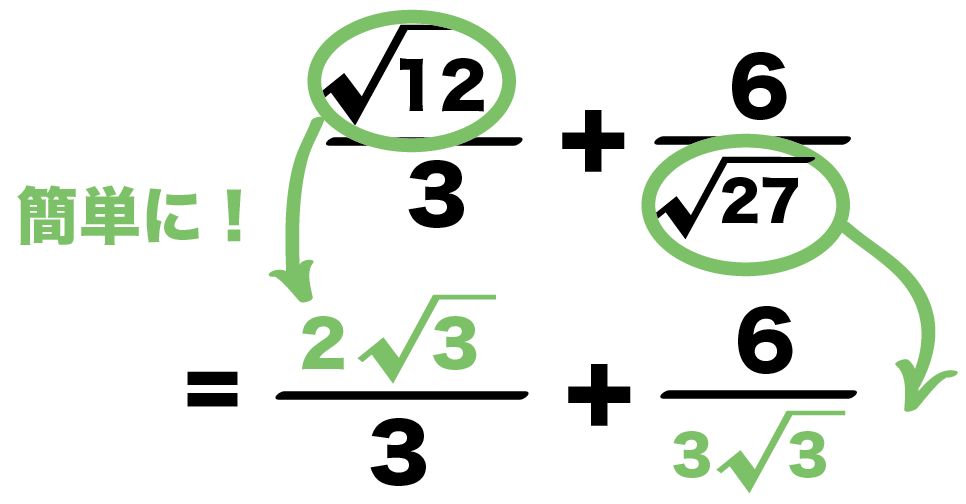



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく




根号をふくむ足し算と引き算 の分数をふくむ場合 Youtube



分数分の分数の計算にルートが入った計算がさっぱりわかりません Yahoo 知恵袋
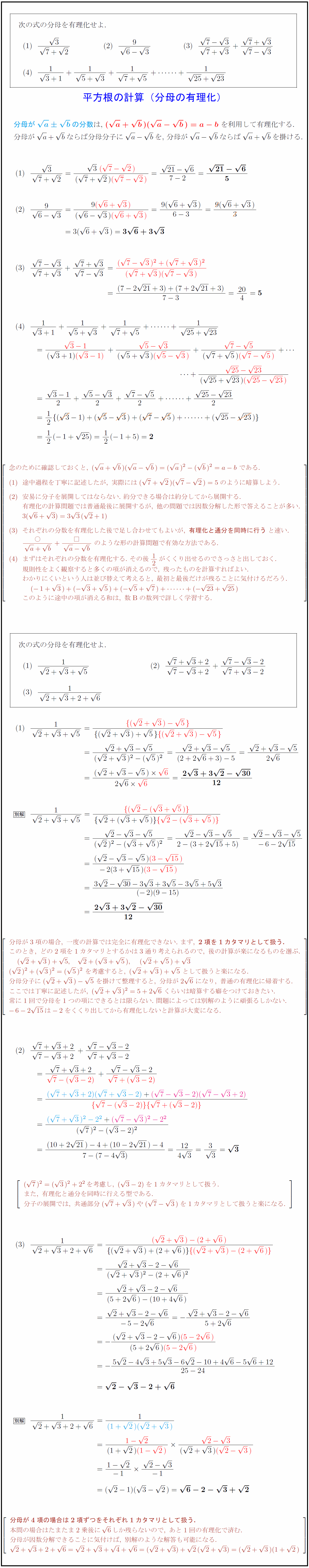



高校数学 平方根の計算 分母の有理化 受験の月
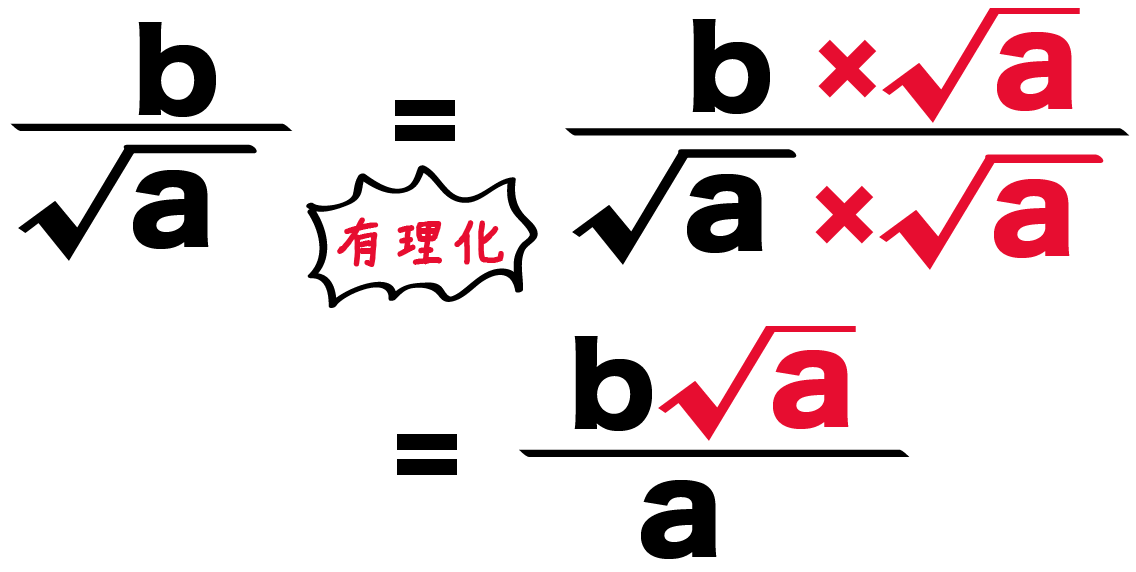



平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学 分母にルートの分数がある場合の計算を教えてください 下の計算 数学 教えて Goo



分子と分母にルートがある分数式の変形 途中の分数の変形が何故こう Yahoo 知恵袋
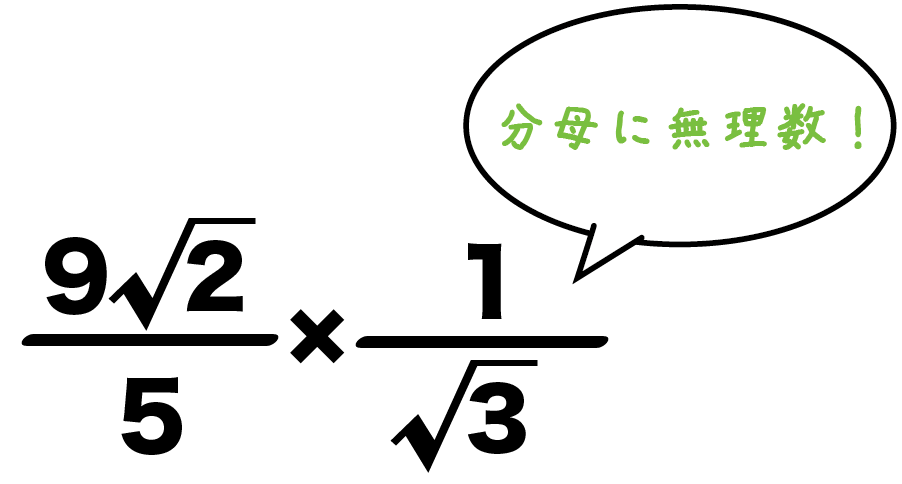



ルート分数の掛け算の計算方法がわかる3ステップ Qikeru 学びを楽しくわかりやすく




平方根 ルート の重要な計算方法まとめ 数学fun



平方根の割り算は 1分でわかる計算 割り算の問題とやり方 有理化 分数との関係




無料印刷可能分数 足し算 引き算 問題 子供のための最高のぬりえ



1




数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo



1



Math 超簡単 有理化 分母に根号がない形にする 働きアリ




数学のルートの分数の二乗 この式の計算方法を教えてください 数学 教えて Goo



Math 超簡単 有理化 分母に根号がない形にする 働きアリ



分数の分母が分数であり その分母がルートの場合の計算の仕方がよくわかり Yahoo 知恵袋



分母にルートが使われている分数が入った計算方法がさっぱり分かりません Yahoo 知恵袋



分数の2乗とは 1分でわかる意味 計算 書き方 との関係




分数を有理化しよう 分母にルートが2つある時はどうしたらいいの さびねこ中学校




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




中学数学 平方根 のコツ 有理化 加減乗除 展開




ルートを分数にできない問題の背理法による証明 高校数学 Irohabook
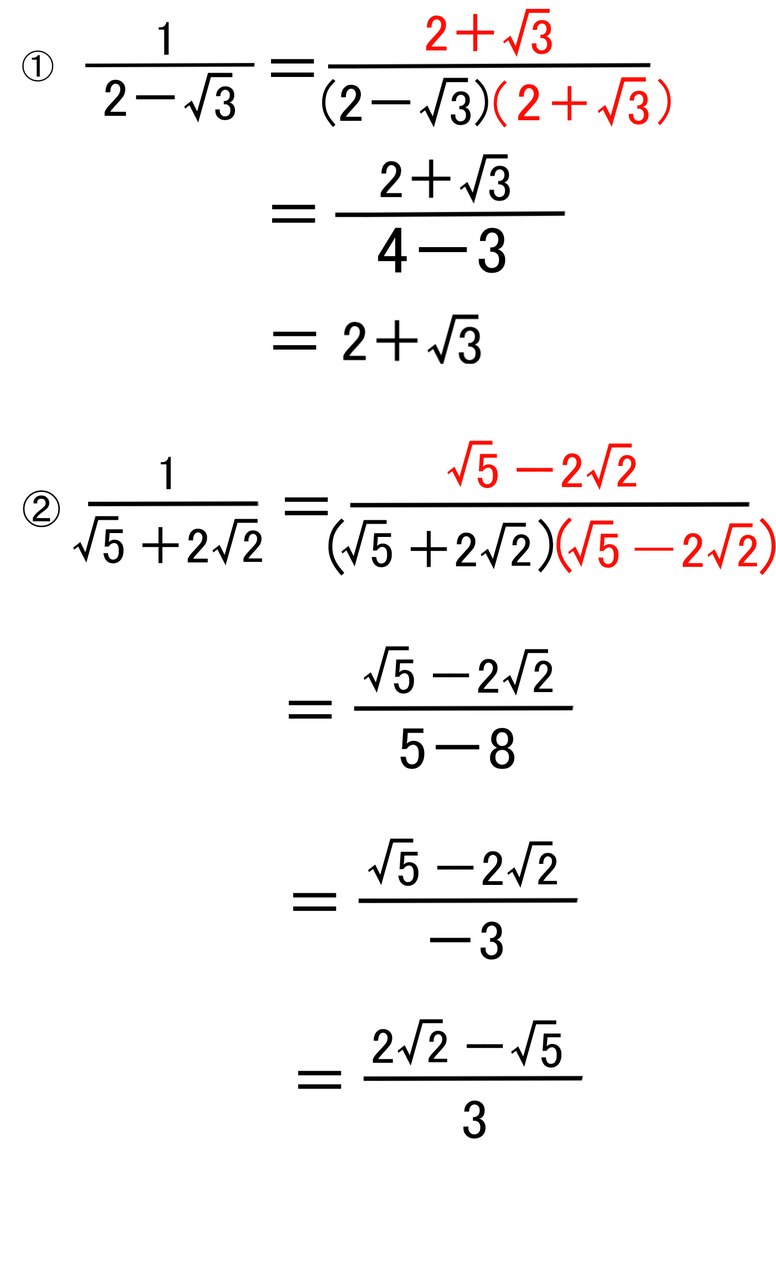



平方根 5 分母の有理化 バカでもわかる 中学数学




数学のルートの分数の二乗 この式の計算方法を教えてください Okwave




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題




中学数学 平方根 のコツ 有理化 加減乗除 展開




複素数の分数の実数化 分母の有理化の複素数版 Irohabook




平方根分野の難所 掛け算と割り算をていねいに あんず学習塾のメモ 図表置き場




平方根 ルート の重要な計算方法まとめ 数学fun




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




このルートが入っている分数がなぜこう約分されるのかわかりません Clear



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス
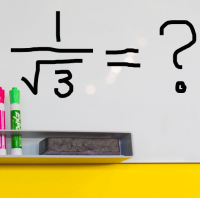



平方根 分母の根号 ルート をなくす 有理化 苦手な数学を簡単に




答えが分数のとき 分母にルートがあったら消す のように分母がマイナスのときはプラスに Clear



この分数分の分数 の計算の仕方がさっぱりわかりません ルートがあるから余 Yahoo 知恵袋




ルート 根号 の計算方法をマスターしよう スタディクラブ情報局




文字の入った分数の約分とマイナスの扱い 分数の文字式の計算 Youtube




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




ルート分数の有理化 項2つ3つある場合は やり方まとめ 高校生 中学数学 理科の学習まとめサイト



平方根 ルート の計算や問題の解き方を完璧に理解しよう Studyplus スタディプラス




複雑なルートの分数の有理化のやり方と問題 理系ラボ




部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ



平方根 分母の有理化のやり方はこれでバッチリ 数スタ




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




平方根 ルート 分数の分母の有理化のやり方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく




数学i 1次不等式 2 4 分母に根号を含む分数の計算 Youtube




小数や分数のルートの外し方 分数の の外し方は知っておくべきだ 中学や高校の数学の計算問題



1



1




ルートの入った計算なのですが この場合って分母に2をかけて分母を消してはダメですよね Clear




有理化とは やり方を分かりやすく解説 練習問題つき 高校生向け受験応援メディア 受験のミカタ




平方根 ルート の重要な計算方法まとめ 数学fun




ルートを分数にできない問題の背理法による証明 高校数学 Irohabook




ルートの計算で分数の分母を有理化しないといけない理由とは さびねこ中学校
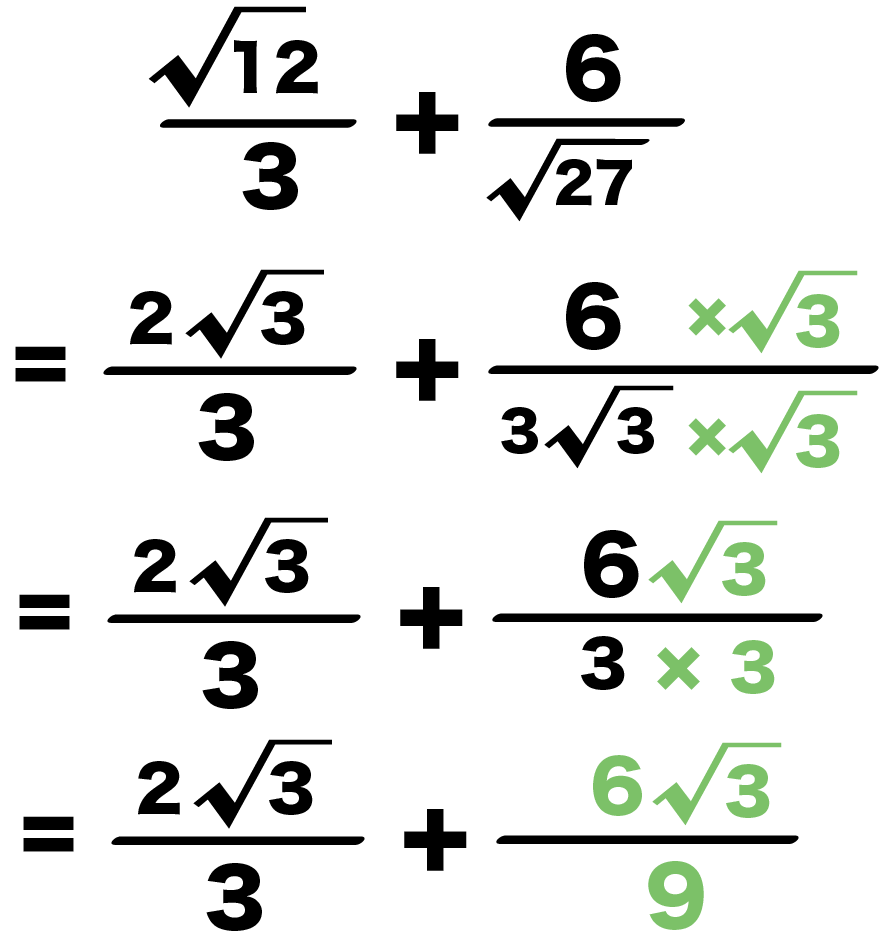



平方根の計算 ルートの分数の足し算 引き算の仕方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
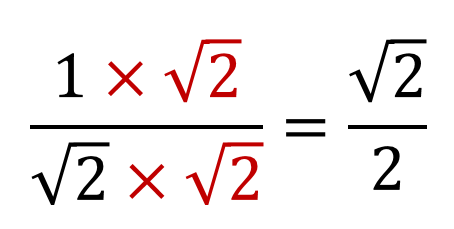



平方根 分母の有理化のやり方はこれでバッチリ 数スタ



高校入試の平方根をたった3分で 得意 にする方法 高校入試徹底対策ガイド




有理化の分数計算 看護受験の必須 数学の公式を確認テスト Vol12 Kazアカデミー 大阪の看護学校 看護予備校




高校数学 数 13 ルート シリーズ 有理化編 Youtube




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題



根号計算 約分




バカでもわかる 中学数学 平方根




割り算をしたとき その数は分母と分子のどっちに行くか覚えよう 中学や高校の数学の計算問題




ルートの分数計算 問題解説で完全マスターだ 数スタ




平方根 ルート の重要な計算方法まとめ 数学fun




分数の計算まとめ 分母が違う分数の足し算 引き算 掛け算 割り算のやり方 アタリマエ




有理化の計算 やり方は 分母のルートを分子にかけるだけ 中学や高校の数学の計算問題



分数関数の不定積分




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




Plumbago 雑記 数学 分数の分母 分子どっちが虚数かで結果が変わるってマジ 平方根 分数 虚数




分母の有理化 Youtube




分母の有理化 分数の平方根で分母のルートを消すやり方 リョースケ大学




ルートの値を代入する問題 色んな知識を使う良い問題です 中学や高校の数学の計算問題



0 件のコメント:
コメントを投稿