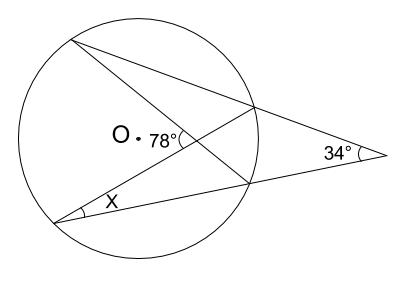
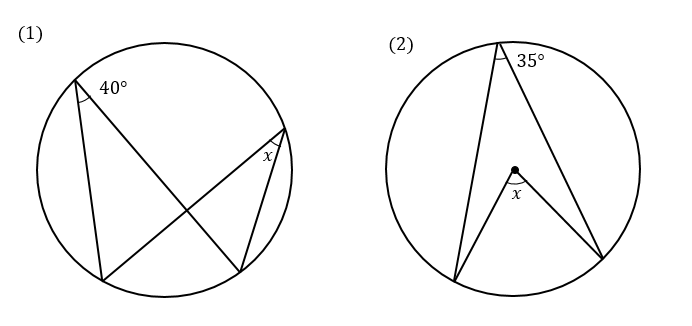
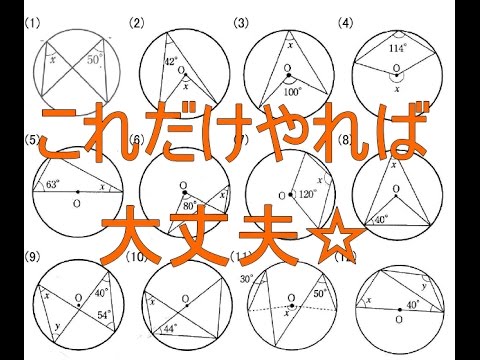
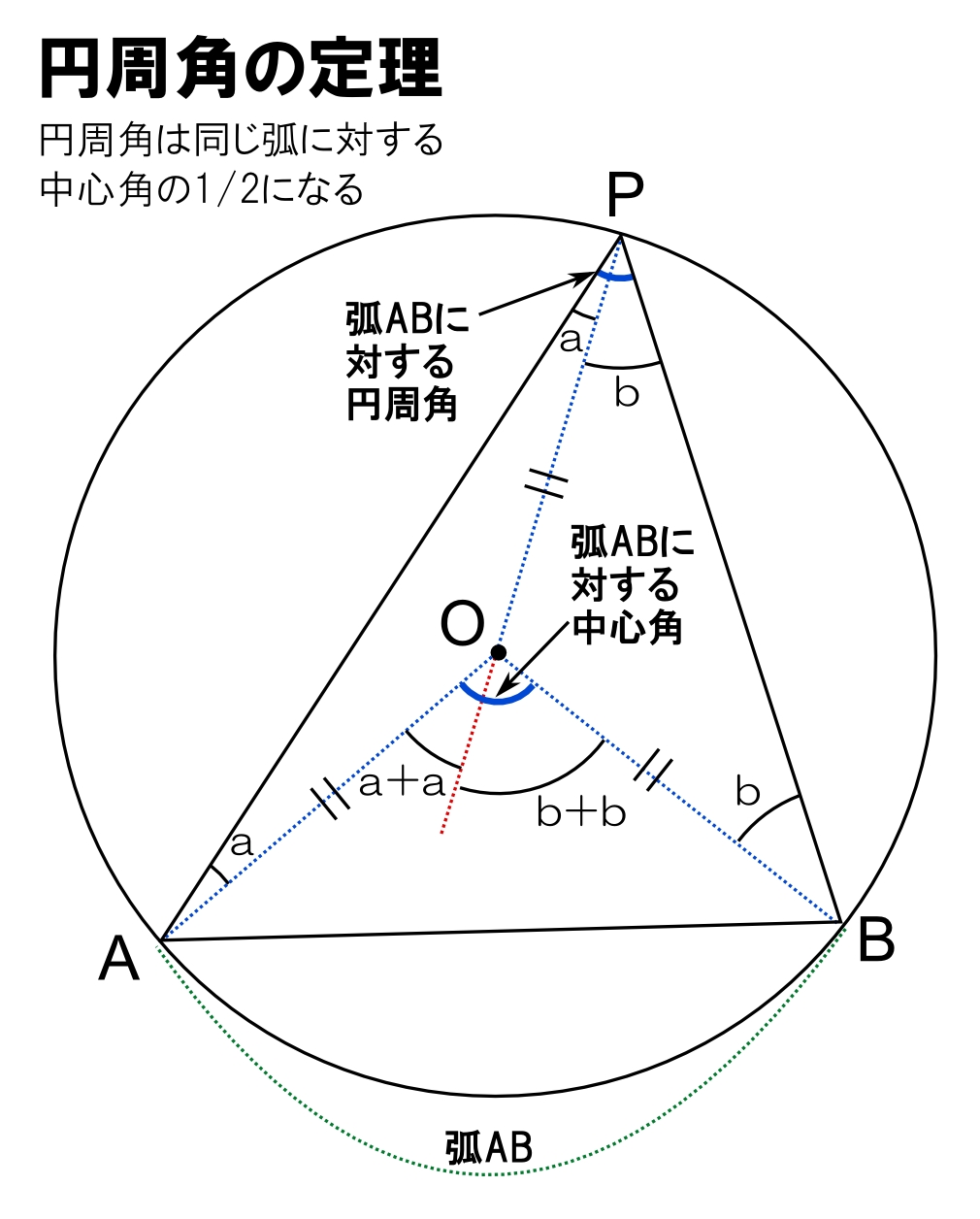
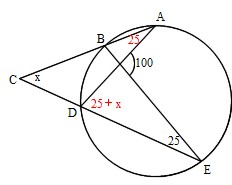
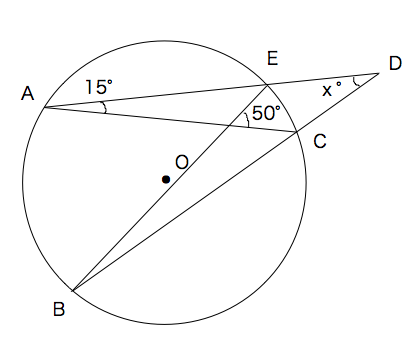
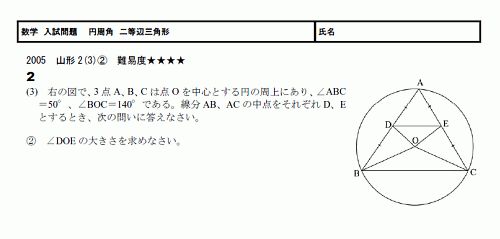
円周角は中心角の半分 同じ弧に対する、 円周角は中心角の半分 だよ。 すると、図の角度が分かるね。 ここから、三角形の 外角の定理 を使うと、 ∠x+50°=100° となるよ。 ちなみに、この三角形の 2辺は円の半径 でできている、つまり 二等辺三角形円周角の定理とは (1)(2)円周角の定理 基本問題解説! (3)(4)見た目がややこしい 問題解説! (5)(6)直径に対する円周角、弧の長さ等しい問題解説! (7)(8)弧の長さと比に関する円周角の問題解説! (9)(10)内接する四角形、接線に関する問題解説! 円周角の問題 中3数学 円周角(ブーメラン型四角形)まとめと問題 円周角の問題を解くとき、円周角の定理がわかっていても、どう解いたらいいのか悩むことも多いです。 今回はそんな円周角の中でも、ブーメラン型の四角形(凹四角形)の円周角について学習します
これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
円周角の定理 問題 難しい
円周角の定理 問題 難しい- ゆうき先生 円周角の定理の逆をつかった問題の解き方3ステップ 円周角の定理の逆を使った問題?? ある日、数学が苦手なかなちゃんは、 円周角や角度に関する問題は、難しい問題を作ろうと思えば作れますが、基本的にやることは同じであることが多いです。 まず、中心Oの有無を確認するといいと思います。ここから色んなことがわかるからです。ひとつひとつ説明します。 円なので一番基本となるのは ①半径が等しい




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学
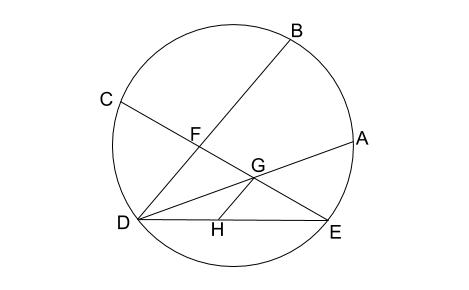
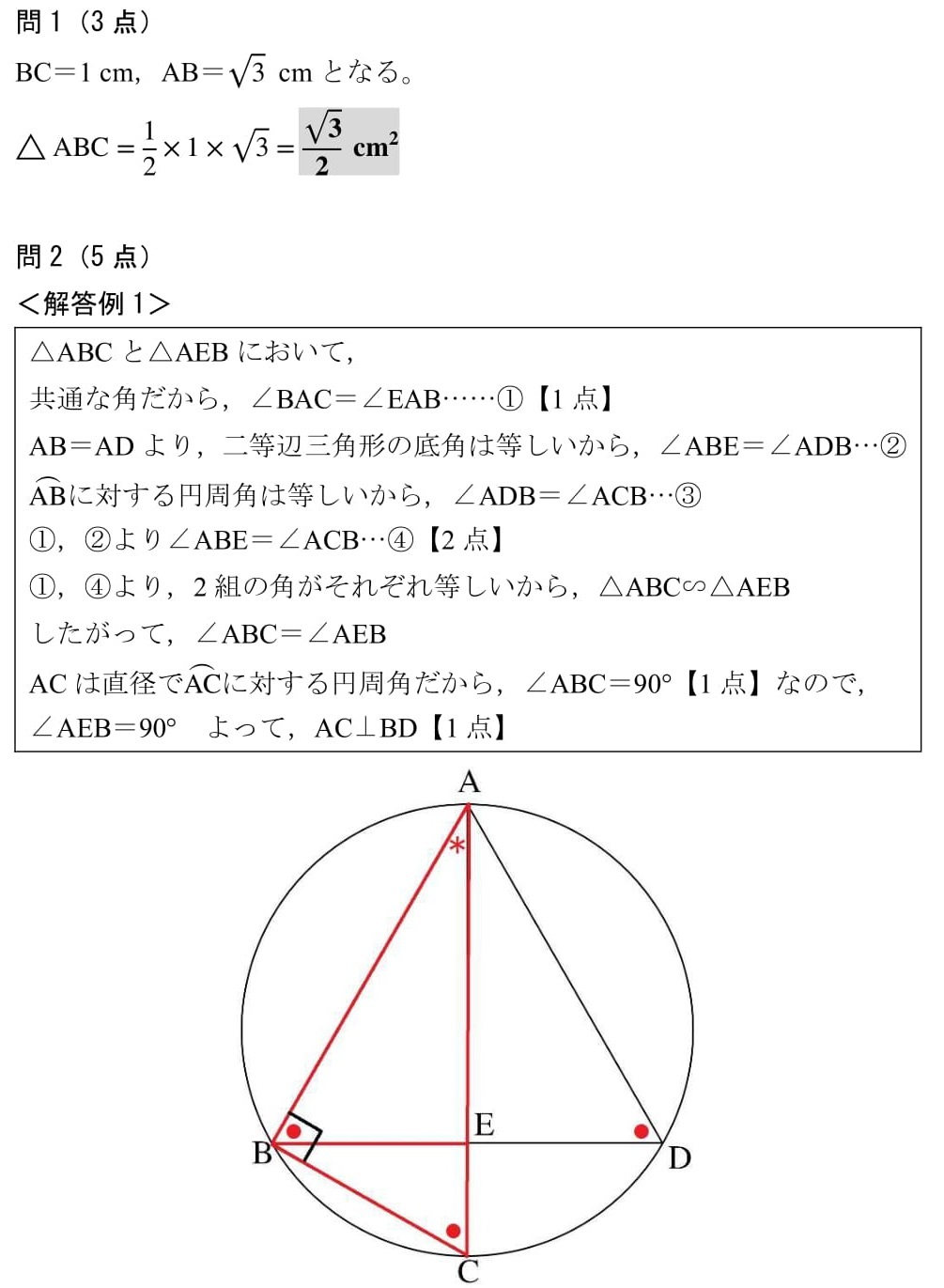
円周角と三平方トレミーの定理が背景? 中学校の定期テストは,基本的にどの先生も出す問題は同じです。 出題の仕方で個性が出たりしますが,基本的にはその先生の授業をしっかり聞いて,対策すれば点は取れるもの。 たまに平均点30点台とか 最後に円周角の定理を使った相似の問題。 相似な三角形を見つけて辺の長さや比を求めていく問題です。 これは結構難しい。 ただ、ある程度問題を解いていると、「この三角形とこの三角形は相似になりそうだ」というのが少しずつ分かってきます。 円周角の定理の逆を使った相似の例 さきほどの続きで直線ACと、直線BDの交点をEと置きます すると、 AEDと BECについて相似を示すことができます。 円周角の定理が使えると、対頂角と合わせることで、簡単に相似は証明できます。
これは他の問題でも非常によく出る図形です。 ※\(\angle ABE=\angle DCE\) も、弧 \(AD\) の円周角より等しいですね。 ここまでは難しいことはありません。普通レベルです。 ここからが本番です。 さて、どうやって解き進めたら良いのでしょうか・・・== 円周角の定理1 == 元のHTML教材 URLhttp//wwwgeisyaorjp/~mwm461/math2/cir101htm PDF版 問題cir101qpdf 解答cir101apdf 戻るこんにちは、家庭教師のあすなろスタッフのカワイです。 今回は、円周角の定理の逆について解説していきます。 円周角の定理について分かっていれば、そこまで難しいことはありませんが、 学校や教科書の説明では少し難しく感じる部分
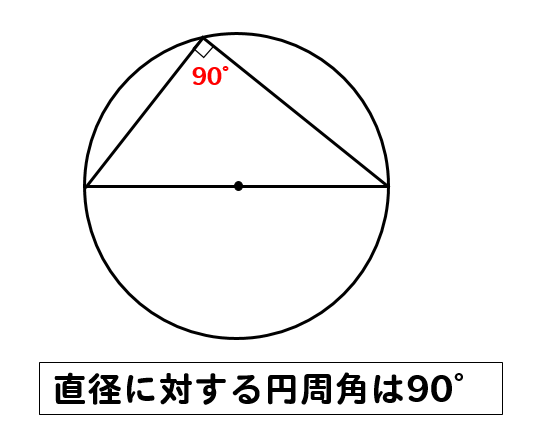
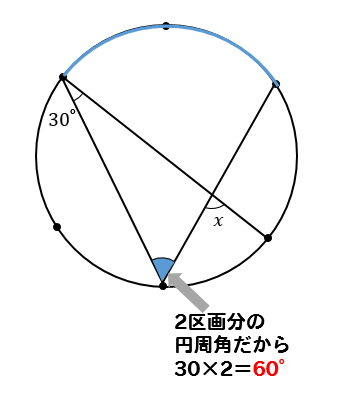
円周角の問題を解くコツ についてまとめます。 3つのポイントに 注意して問題に取り組むこと。 1.弧に注目する 2.直径が出てきたら 90°の円周角を探す 3.補助線を引いてみる 「できる」と自分を信じて1次関数,円周角と三平方,整数問題 ・12年度(★★★★☆) 難易度が落ち着きました。 2次方程式整数問題,円周角角度問題,1次関数 ・13年度(★★★★☆) 露骨に簡単な問題と,露骨に難しい問題があります。点差つかないかも。三平方のごりおし。またまた円周角の問題。 円周角の問題ってパターンが限られるところがあるので、2問も出題されたのは少し驚きました。 さすがに少しひねった問い方をしていますが、さほど難しい問題ではありません。 というかこれ、円周角の定理の逆だろうということ



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
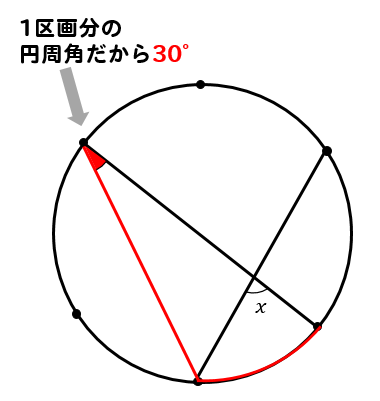
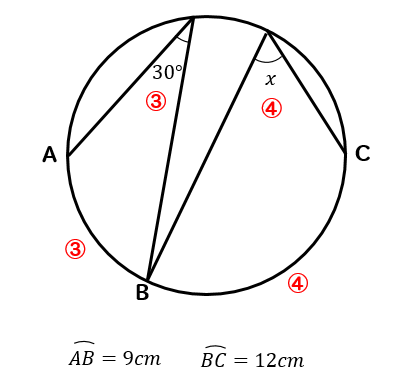
== 円周角の定理 ==(応用問題) 《問題》 次の角a,b,c,...の大きさを求めなさい. (1) a= (2) b= 図の赤で示した弧に対する円周角は等しいから,黄色で示した三角形の1つの角が30°だと分か 「円周角の定理」も小学校で習う算数から導かれる このように、難しいと思われた「円周角の定理」も、「三角形の内角の和は180度になる」という小学校で習う単純な三角形の特性から導くことができるのです。 また数学の問題や証明には、パスルを場面を取り上げることはほぼないと感じる。そこで円周角の定理を用いた証明問題を取 り上げる。本論文は,その教材及び実践内容,それに対する考察を報告するものである。 <キーワード>円周角,三角形の外角の性質,図形,証明,サッカー 1.はじめに



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
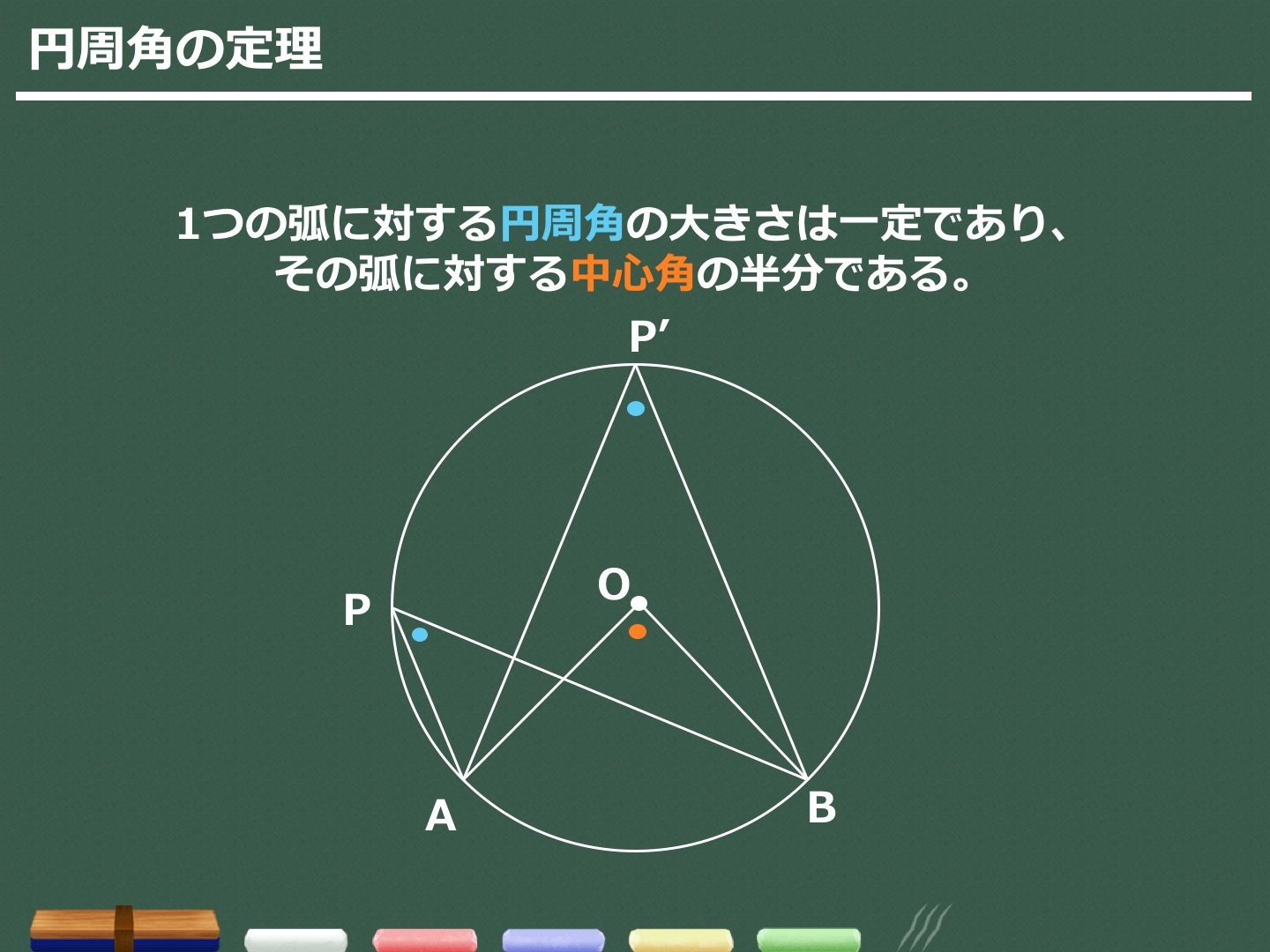
Title FdData中間期末過去問題中学数学3年(円周角と中心角/円周角の定理/接線) Author Fd教材開発 Created Date 単元 円周角の定理(円周角と中心角),円周角の定理の利用, 「数学 超難問 暇な時などにやってみては?」, 学年 中学3年生, キーワード 数学,超難問,kikinote,math円周角 三角形の外角の関係を使う問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 三角形の外角は それと隣り合わない2つの内角の和に等しい。




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




超難問 角度問題です エレガントな解法が出来ません 下の図で X 数学 教えて Goo
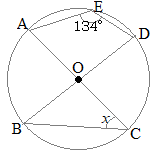
円周角と中心角(2) 円周角と中心角(3) 等しい弧と円周角 円周角と図形の証明 円周角の定理の逆 円周角の定理の活用 7 三平方の定理 三平方の定理の証明(1) 問題一括 (3,793Kb) 解答一括 (4,569Kb) 三平方の定理の証明(2) 三平方の定理の証明(3) 三平方の定理(15円周角の定理 ちょっと難しい問題に自分の表現を見直させたりする。 定理の確認 着かない生徒には個別指導を行う。 (2)練習問題3 定理やいろいろな性質を使って角円周角と中心角の関係や、それを証明する方法を理解し、円周角の定理を活用する問題を繰り返し練習します。 円周角の定理(1) ⇒ 答え 円周角の定理(2) ⇒ 答え ⇒ 大問1の (2)の「円に内接する四角形の性質」を用いた場合の解説はこちら 円周角の



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ
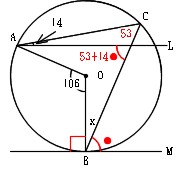
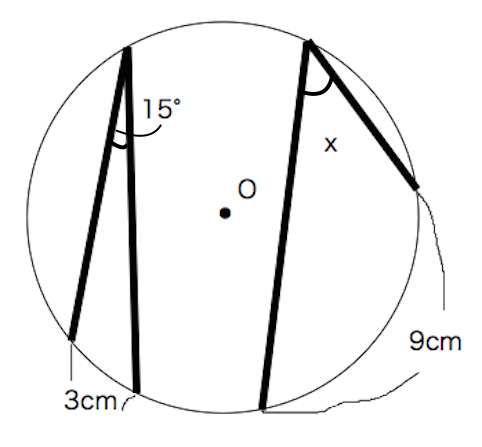
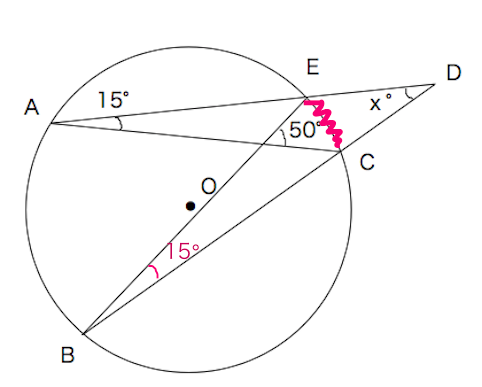
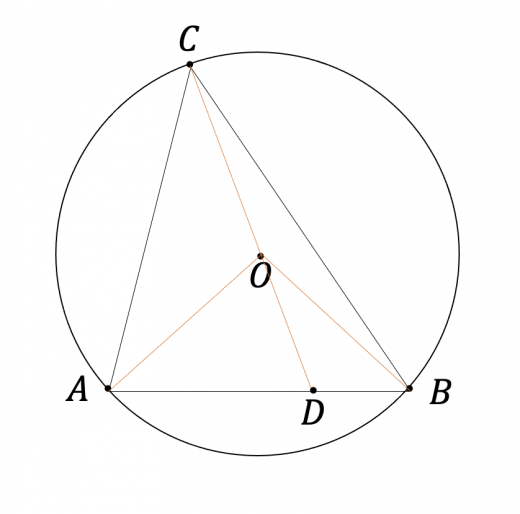
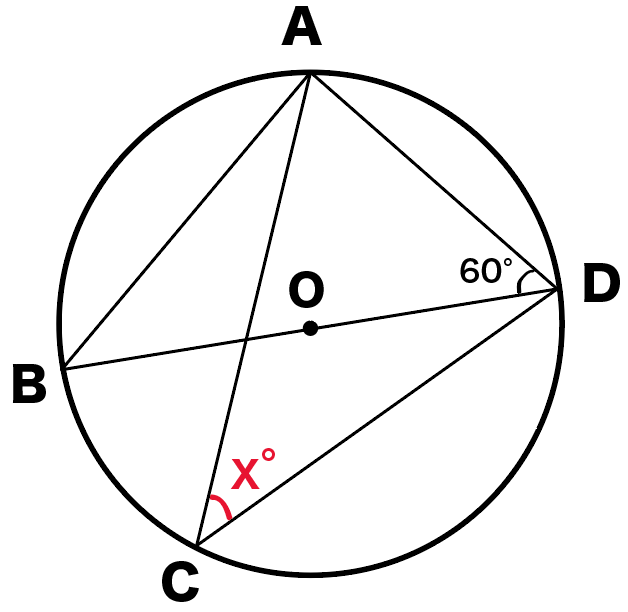
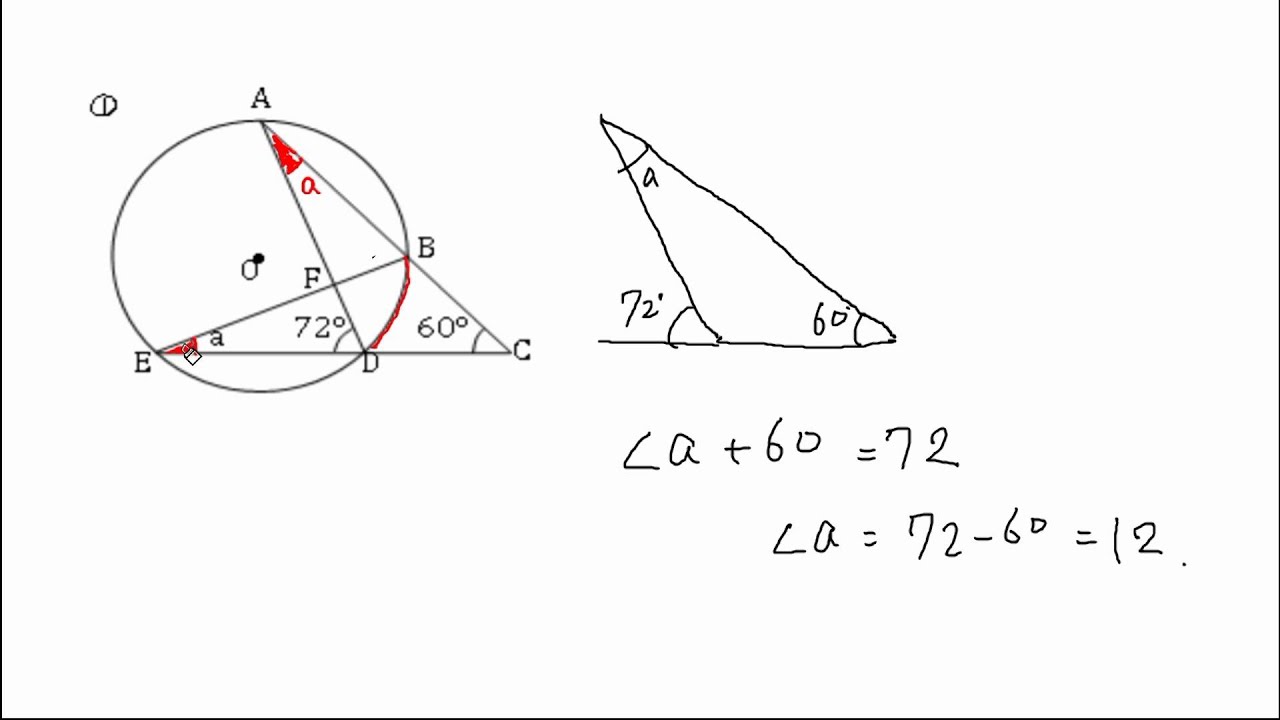
教訓2:悩んだら、 中心角 をかき込む 例題5: 一部の直線が円からはみ出した問題です。 この種類の問題は、円周角の定理を使ってわかる角度を記入したあと、三角形の角度の問題で一番よく使う、ある技を使うと解けます。 (気づこう) (かき込み)円周角 補助線を引く問題 円周角の定理 1つの弧に対する円周角の大きさは一定であり、 その弧に対する中心角の半分である。 2つの半径OA, OBと弦ABによって できる三角形は必ず二等辺三角形になる。 A B O 中心Oに向かって補助線をひき、二等辺三角形や 円周角の定理の逆とは? 次に、「円周角の定理の逆」について説明します。 逆って何?と思った方もいるでしょう。「円周角の定理の逆」とは、 図で表すと、以下のときは、 a,b,p,qが円周上にある、ということです。 なぜこうなるのか説明する前に、




の求め方を教えて下さい 一問だけでも大丈夫です Clear



円の総合問題 その5 相似の利用の難問 中学数学の無料オンライン学習サイトchu Su
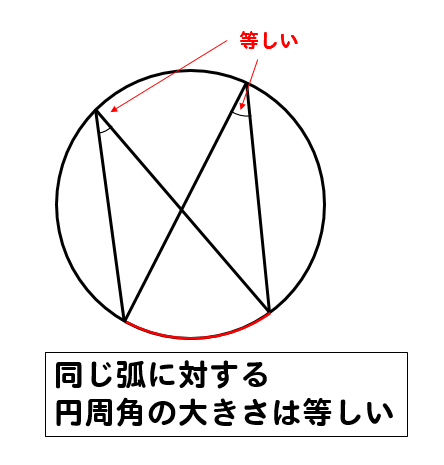
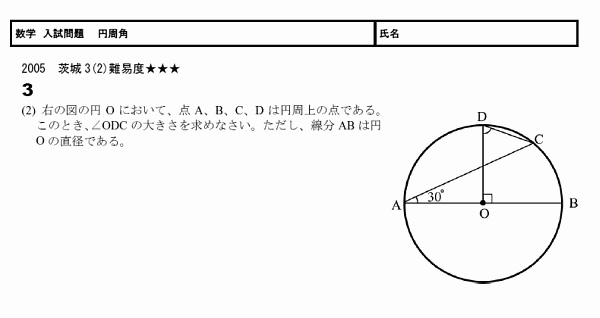
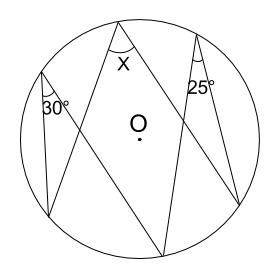
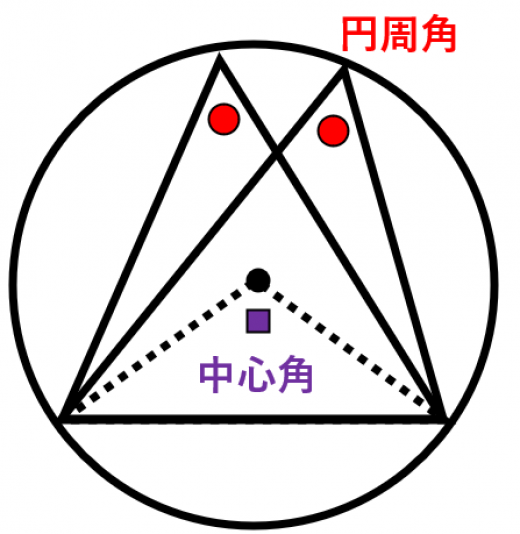
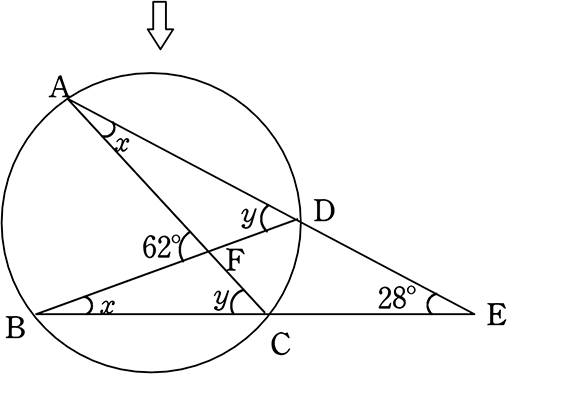
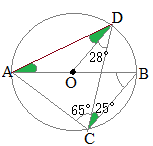
①円周角の定義を知る。②円周角や中心 角を測定し,円周角の定理を予想する。③パソコンで予想を確かめる。④証明の場合 分けを考える。⑤補助線を入れて証明をする。 ②において,分度器で測定することにより,円周角の定理を予想させる。固定の図一般に,高校入試問題では「円周角の定理」を覚えているだけでは,問題は解けません.この問題では,次の2つの定理を組み合わせて解いています. (1) 二等辺三角形の2つの底角は等しい. (2) 円周角は中心角の半分になる. 特に, (1)を使って元の角 xまずは、円周角の定理をおさらいしておきましょう! 同じ弧に対する中心角の大きさは円周角の大きさの2倍になる。 同じ弧に対する円周角の大きさは等しい この2つは円周角の定理の基本です。 必ず覚えておきましょうね! そして、次はブーメラン型



円周角の定理 練習問題 苦手な数学を簡単に




中学数学 円周角 中心角
明らかに、「\(2\) つの角が等しい」から相似を示すしかありません。 目標の \(2\) つの三角形から、どこの角が等しいと言えそうか見てみます。 青い角は「共通なので」等しいです。 あと \(1\) つです。 このような問題では、円周角に着目するしかありませ円周角の定理 ・ 円周角の定理から派生する定理 ・ 例題問題 円周角の定理を利用して色々な角度を求めてみる ・ ここまでの各定理の証明 → 接点までの距離は等しいという証明 → 円周角の定理の証明 → 弧と円周角の定理の証明 ② 円周角の定理の逆 と 円周角の定理に関する基本的な問題です。基本事項下の図のように 一つの孤に対する「円周角」の大きさは,「中心角」の半分になります. 同じ弧に対する円周角は等しくなります。覚えるのはこの2点だけです。 このような形になっている場合も円周角は中心角の半分になります。



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ
円周角の定理を使った練習問題です。ここで差がつく! 円周角の定理がさまざまあるので、問題文からキーワードを読み取り、定理・性質を活用して解きましょう。 キーワードになりえるもの直径、内接する四角形、弧の比、共通する弧など 今回使う公式(円




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



高校入試 数学 無料学習プリント教材



1




数学 中3 56 円周角の定理 基本編 Youtube



円周角の定理 入試問題



円周角の定理と中心角 中学3年数学 Youtube
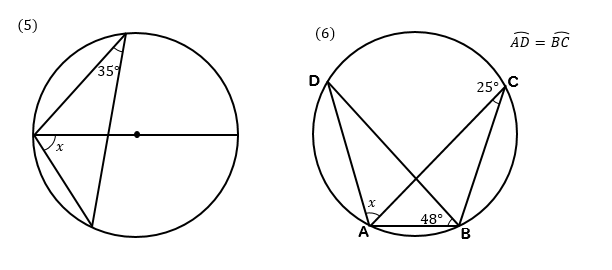



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
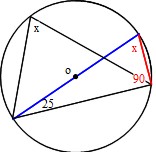



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ
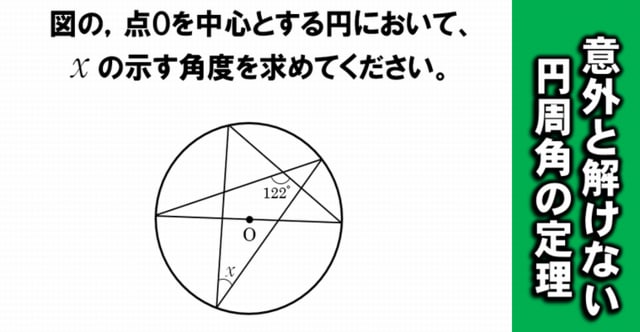



意外と解けない円周角の定理 中3レベルの数学問題 暇つぶしに動画で脳トレ




円周角の定理で よく補助線引きますよね その補助線を引く場所がよく分かりません 円の Clear




これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



中3数学 パターン確認 円周角と相似 個別指導塾のyou 学舎日記 公式ブログ




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
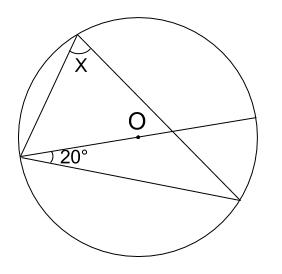



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



あなたは3秒で解けますか ビジネスに役立つ論理思考を 中学数学 で鍛える Sbcr Online




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




円と角度のチェックテスト2 円周角を求める発展問題 難しい問題もあります Youtube




円周角



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ




数学問題 大人は意外と悩んでしまう円周角の定理 暇つぶしに動画で脳トレ




中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



1



円周角の定理 練習問題 苦手な数学を簡単に
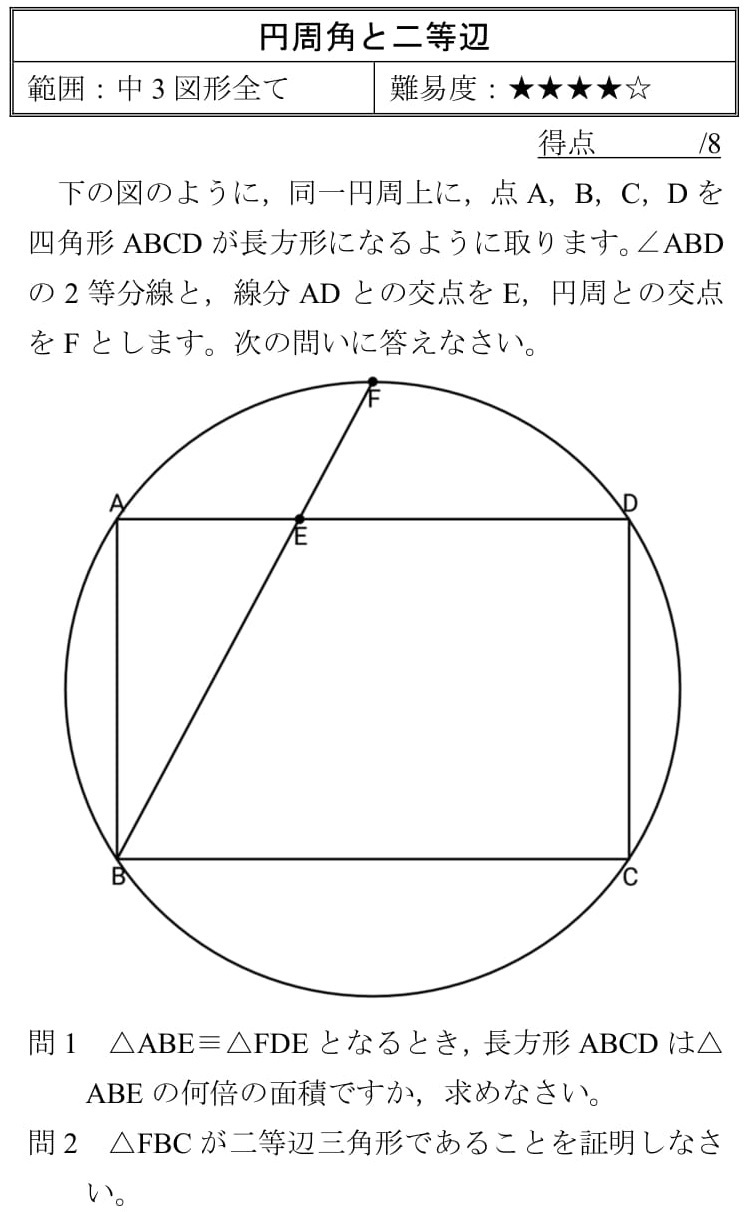



円周角と二等辺三角形 オリジナル 高校入試 数学 良問 難問



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス



数学の問題 解き方と答えを教えてください 円周を12等分す Yahoo 知恵袋
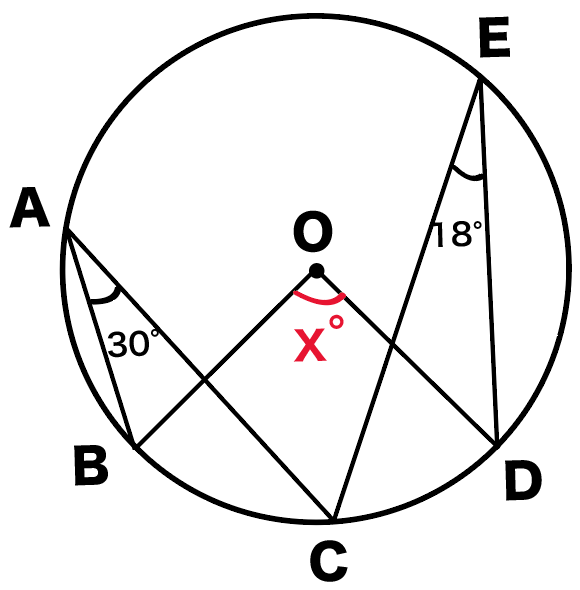



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく
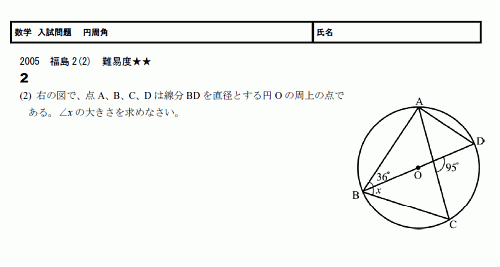



数学 高校入試 無料学習プリント教材




図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
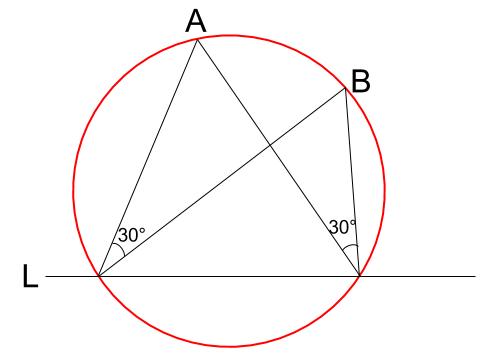



30 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su



中学数学 円周角の定理 例題その3 中学数学の無料オンライン学習サイトchu Su



円周角証明の究極系 オリジナル 高校入試 数学 良問 難問



円周角の定理の解説 問題の解き方 数学fun



円周角の定理 練習問題 苦手な数学を簡単に




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学




数学 中3 57 円周角の定理 少し応用編 Youtube



Math 円 4 円周角の難しい問題を解くコツ 働きアリ The 2nd



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



円周角の定理の証明の問題です 次の図で Ab平行cdならば 孤ac 孤bdで Yahoo 知恵袋
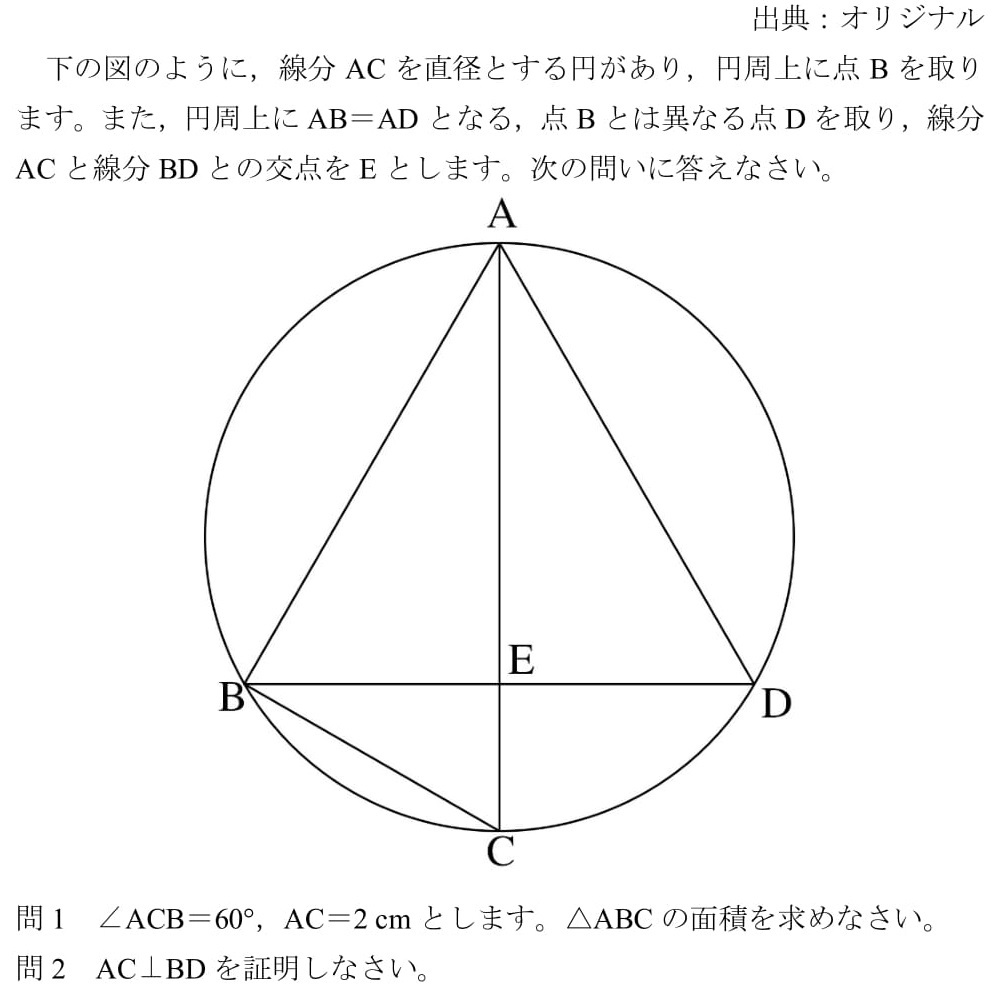



円周角証明の究極系 オリジナル 高校入試 数学 良問 難問




接弦定理とは何か 角度別に分かるその証明方法 アタリマエ



3分でわかる 円周角の定理とその逆の証明 問題の解き方 合格サプリ



中学3年数学 弧と円周角の定理次の図でxの値を求めなさい 求め方を教え Yahoo 知恵袋



Xirndkzkljhwjm



数学 高校入試 無料学習プリント教材




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所




Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



1
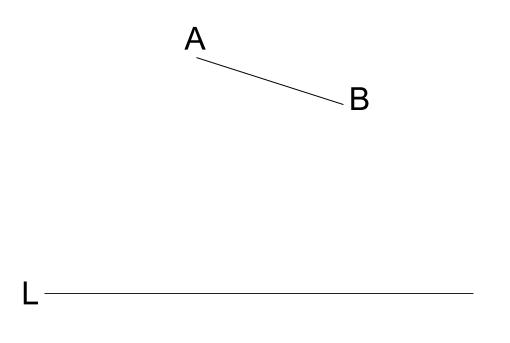



30 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su




円周角の定理の逆はなぜ成り立つのか 証明と問題の解き方とは 遊ぶ数学



中学数学 円周角 中心角




円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく




円周角の定理はこれで完璧 定理の証明と様々な問題の解法




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所




円周角の定理を使わずに解け 中学受験 算数 数学 難問 小学生 中学生 Youtube




高校数学a 共円条件 4点が同一円周上にある条件 受験の月



Xirndkzkljhwjm



円周角の問題です これは 円周角の定理の逆を使って 点fを中心と Yahoo 知恵袋



円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく



円周角の定理 入試問題



数学 中学3年生 円周角と中心角の教え方のコツ なるほど 塾講師が教える教え方のコツ




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん
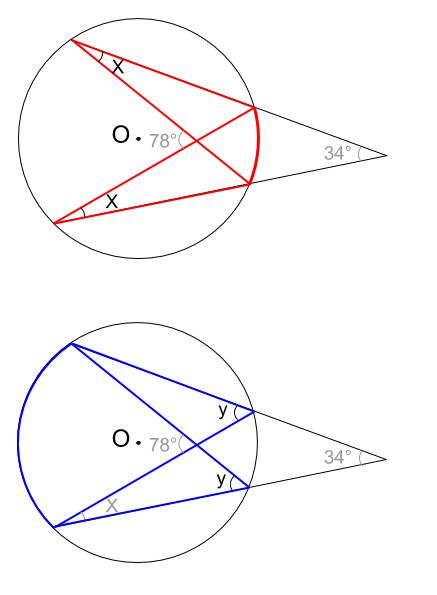



中学数学 円周角の定理 例題その4 中学数学の無料オンライン学習サイトchu Su




円周角の定理の逆をつかった問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく




数学の成績を上げる方法 円周角の問題を数秒で解くコツ
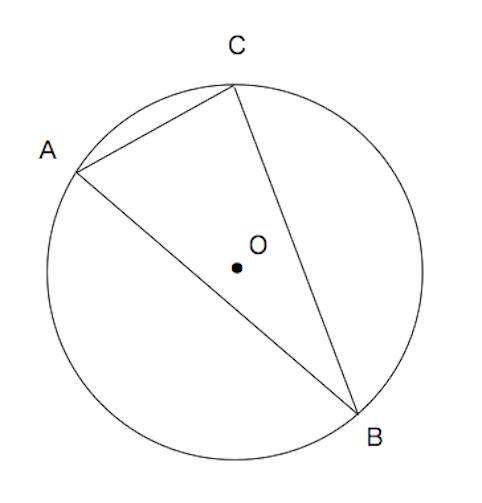



円周角の定理 練習問題 角度がわからない 苦手な数学を簡単に
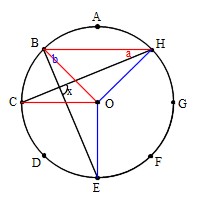



Mathematics 円 4 円周角の難しい問題を解くコツ 働きアリ



Studydoctor円周角の定理と中心角 中学3年数学 Studydoctor



円周角の定理は人生の縮図 円周角の定理が苦手な子どもへの処方箋 子どもの夢を叶える心理作戦
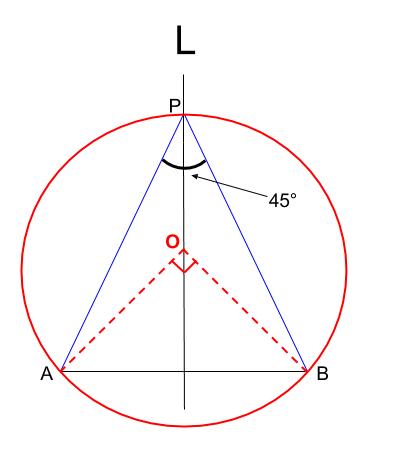



45 の作図 円周角の定理の利用 中学数学の無料オンライン学習サイトchu Su
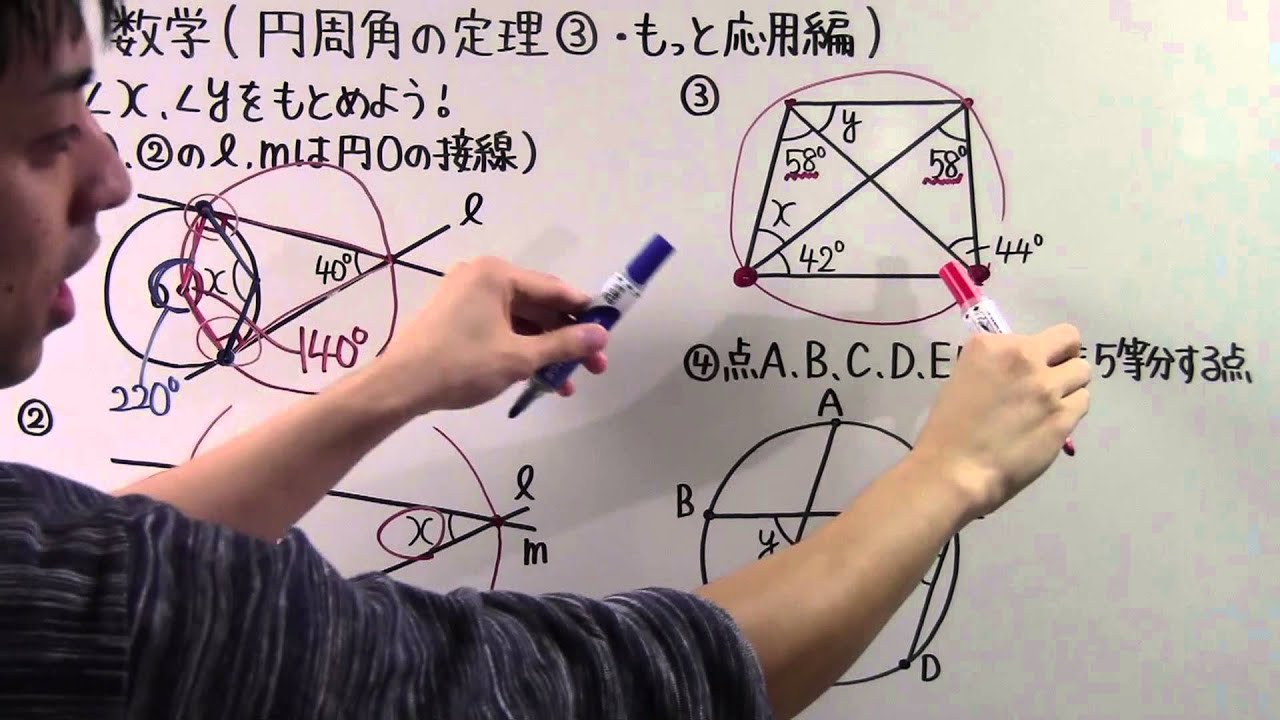



数学 中3 58 円周角の定理 もっと応用編 Youtube



円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス
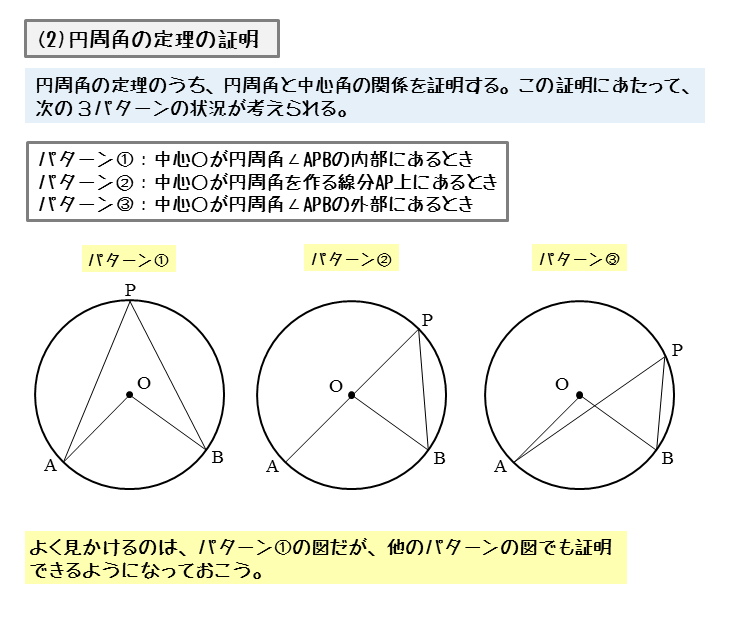



図形の性質 円周角について 日々是鍛錬 ひびこれたんれん




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ




円周角の定理の基本 計算 無料で使える中学学習プリント
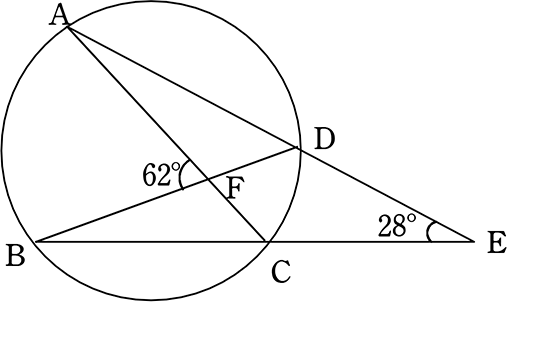



中学数学 円周角 中心角




円周角の定理はこれで完璧 定理の証明と様々な問題の解法




円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ
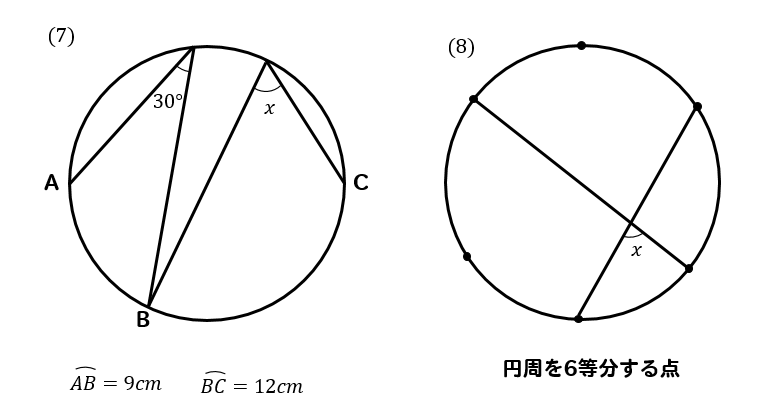



これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ




これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ



中学3年の数学の円周角の定理問題なのですが よくわからな Yahoo 知恵袋




中3数学 円周角の定理 良難問とその解説 定期テストや高校入試に レオンの中学数学探検所



1



円周角の定理 問題 Youtube



0 件のコメント:
コメントを投稿